|
¿Qué relaciones se establecen?
Características numéricas. Relaciones
A continuación vamos a detallar actividad matemática
que se ha desarrollado con estudiantes para maestro en el contexto de
una clase de Laboratorio escolar de matemáticas (asignatura del
currículum en vigor), utilizando como situación de partida
la tarea de investigación que se muestra en el cuadro. Los estudiantes
para maestro a los que se hace referencia estaban trabajando en uno de
los grupos en los que se distribuye la clase y se han nombrado con E1,
E2, E3 y E4. La P hace referencia a la profesora.
Los interesados en conocer la actividad anterior que se
ha desarrollado para Buscar las características
numéricas y su disposición en el espacio cuando los modelos
se apoyan en diferentes elementos, pulse en esta opción.
| Tarea de Investigación |
| a) |
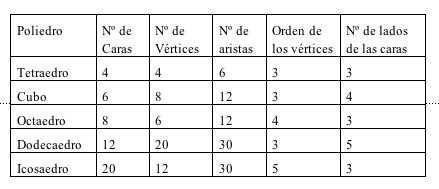
Recopilar en una tabla las características
numéricas (relativas al número de elementos: C, V, A)
de los poliedros regulares así como el orden de los vértices
y el número de lados del polígono de sus caras.
A continuación enunciar relaciones entre el número de
elementos de determinados pares de poliedros, entre el número
de diferentes elementos de un mismo poliedro, y también otras
relaciones numéricas que encontréis. |
| b) |
Agrupar los enunciados expresados en a) que penséis
que pueden corresponder a problemas análogos.
Tratar de delimitar así algunos problemas con los que podríamos
continuar el estudio de los poliedros regulares.
Observar también si surgen problemas que hemos tratado ya
en clases anteriores. |
Después que se distribuyera a los estudiantes la
tarea de investigación y se planteara como tarea para resolver
ese día en clase, ésta se condujo como sigue:
| {1} |
P: En la tabla yo he ordenado los poliedros
regulares como Tetraedro, Cubo, Octaedro, Dodecaedro e icosaedro.
¿Qué criterio he utilizado en mi ordenación?
|
| {2} |
E1: Están en orden por el número de
caras. |
| {3} |
P: Si la primera columna la encabezáramos con los vértices,
¿qué ordenación pondríais para los poliedros
regulares? Bueno, esto para casa. Si queréis, podéis
mirar a ver si se facilita o no el desarrollo de la actividad con
una ordenación u otra, y si diferentes ordenaciones conducen
a la misma o a diferente actividad. Ahora ya tenemos los encabezamientos,
vosotros rellenar vuestra tabla, las características de los
poliedros las tenéis en los apuntes. También podéis
determinar éstas de nuevo, contando por niveles. Yo voy a
hacerlo en la pizarra.
Rellena la tabla rápidamente dirigiéndose a los alumnos]
Para el tetraedro: tetra..4, El cubo, Hexa, 6, Octa 8, 8, dodeca
12, icosa 20. Para el tetraedro, triángulo, 3, para el cubo
cuadrado, 4, octa, triángulo, 3, dodeca pentágono,
5, icosa, triángulo 3. A ver, 4, 4; 6, 6; 8, 8; 3, 3; 4,
4; 5, 5; 3, 3. Y aristas, a ver..3,3, 6; 4, 4, 4, 12 y 12; 5, 5,
10, 5, 5, 30 y 30. ¡Ya la tengo!
|
Como cabe esperar, cuando el profesor acaba de rellenar
la tabla en la pizarra, los estudiantes apenas han rellenado las características
de uno de los poliedros. Más aún si tenemos en cuenta que
algunos estudiantes se ponen a buscar en sus apuntes los resultados obtenidos
en las clases anteriores. Después de hacerles notar de que para
resolver esa cuestión sólo tendrían que disponer
de más tiempo, bien para repetir cada actividad que ya realizamos,
bien para que puedan encontrar los resultados obtenidos en los apuntes,
indicamos que al final de la clase se podrá rellenar la tabla rápido
aplicando relaciones entre poliedros que se van a descubrir. La actividad
se dirigió como sigue:
| {4} |
P: Vale, como supongo que algunos aún
no habeis rellenado totalmente la tabla, mirar la que tengo en la
pizarra (y si ya la tenéis mirar la vuestra). Ahora vamos
a pasar al siguiente problema que plantea la tarea de investigación
en el apartado a).
Tarea de investigación
a) Recopilar en una tabla las características
numéricas (relativas al número de elementos:
C, V, A) de los poliedros regulares así como el orden
de los vértices y el número de lados del polígono
de sus caras.
A continuación enunciar relaciones entre el número
de elementos de determinados pares de poliedros, entre el
número de diferentes elementos de un mismo poliedro,
y también otras relaciones numéricas que encontréis.
b)Agrupar los enunciados expresados en
a) que penséis que pueden corresponder a problemas
análogos.
Tratar de delimitar así algunos problemas con los que
podríamos continuar el estudio de los poliedros regulares.
Observar también si surgen problemas que hemos tratado
ya en clases anteriores. |
¿Qué relaciones encontrais en la tabla? Pensar ..
a ver... Posibles respuestas... Después de la observación
que hagais intentar construir un enunciado que refleje esa observación.
|
| {5} |
E1: ¿Qué tenemos que mirar? Yo no entiendo
lo que preguntas... |
| {6} |
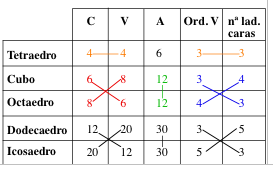
P: Fijaos en los números que hay en las casillas
y después tratar de expresar lo que observéis haciendo
referencia a las características numéricas de los poliedros
implicados. Por ejemplo, en la tabla veo un 8 que hace referencia
a los vértices del cubo. Y veo otro 8 que hace referencia a
las caras del octaedro. Así, el número de vértices
del cubo coincide con el número de caras del octaedro. |
| {7} |
E1: Yo observo que hay un seis y un seis. El número
de caras del cubo y el número de vértices del octaedro. |
| {8} |
E2: El seis también está en el tetraedro.
En las aristas. |
| {9}: |
E3: Las aristas de ellos son las mismas también.
Del cubo y del octaedro. |
| {10} |
P: Fijaos sólo en el cubo y el octaedro, juntar
con un segmento los elementos que sean iguales y después dar
enunciados que indiquen todo lo que podemos apuntar. |
| {11} |
E4: Sale una cruz y una raya. Las caras son los vértices
y al revés. Las aristas son las mismas. |
| {12} |
P: Vale, en el cubo y octaedro el número de
caras y de vértices se intercambia y el número de aristas
coincide. ¿Se puede decir algo sobre el orden de los vértices
y el número de lados del polígono de las caras? |
| {13} |
E2: También sale en cruz. También se
cambia. |
| {14} |
14} E1: En el dodecaedro e icosaedro también
salen dos cruces y una raya para las aristas. Sale lo mismo. Las
caras son iguales que los vértices y las aristas las mismas
y las caras y los vértices de orden también.
|
| {15} |
P: Fijaos en otro par de poliedros.

|
| {16} |
E4: En el tetraedro y el cubo el 6 está en...
Las aristas del tetraedro y las caras del cubo... son las mismas |
| {17} |
P: El número de aristas del tetraedro coincide
con el número de caras del cubo. ¿Habíamos visto
ya este resultado? |
| {18} |
E4: En el cubo y dodecaedro también, las aristas
del cubo y las caras del dodecaedro... Si ya lo hemos visto en otra
clase y al final lo veía, pero yo ahora no me acuerdo. Si no
nos lo enseñas otra vez... |
| {19} |
E1: El número de aristas del tetraedro coincide
también con el número de vértices del octaedro. |
| {20} |
E2: Y el número de aristas del cubo con el
número de vértices del icosaedro.

|
Cuando en diferentes sesiones con estudiantes para maestro
se ha tenido dificultad para resolver la tarea, algunas sugerencias que
han ayudado a los estudiantes centran la atención en la representación
visual de relaciones que se observan, aclaran la estructura de los enunciado
para facilitar que se enuncien verbalmente las relaciones que se han indicado,
se sugieren los elementos que se han de considerar para enunciar otras
relaciones o se apunta que se establezcan relaciones entre otros pares
de poliedros.
En la conversación que hemos transcrito cabe señalar
que en {10} se indica que se representen las relaciones visualmente y
luego que se enuncien verbalmente; en {12}el profesor enuncia la relación
de manera precisa y dirige hacia relaciones entre el orden de los vértices
y el nš de lados de las caras; en {15} centra la atención en relaciones
que implican otros poliedros; y en {17} se dirige ya a que relacionen
lo que se está haciendo con lo trabajado en otras clases.
Respecto del uso que se hace del lenguaje geométrico
y de la precisión con la que se enuncian las relaciones es importante
aclarar que en las intervenciones que hacen los estudiantes en las puestas
en común, en muchas ocasiones el profesor no corrige la expresión
para que no perturbe otras ideas interesantes que los estudiantes puedan
expresar. Sugiere que centren atención especial en ello una vez
que tengan expresada una relación o una propiedad. Insiste en que
una vez escrita en el papel se revise de nuevo prestando la atención
ahora en enunciarla de manera precisa.
En algunas clases se expresan también relaciones
numéricas que dan unos elementos en función de otros; por
ejemplo, que el número de caras del tetraedro más el número
de vértices es igual al número de vértices del cubo,
o que el número de aristas de un poliedro regular se obtiene multiplicando
su número de caras por el nš de lados de sus caras y se divide
entre dos (porque cada arista pertenece a dos caras). También es
usual que algún estudiante elabore la fórmula de Euler:
C+V=A+2.
Asimismo pueden surgir otras cuestiones interesantes como,
por ejemplo, la que indicó uno de los estudiantes: “Mira
lo que se me acaba de ocurrir. Tenemos modelos del tetraedro en el cubo
y del cubo en el dodecaedro. ¿Al revés puede ser? ¿Se
puede inscribir el poliedro circunscrito en el inscrito?
Por lo que a
Por lo que a partir de la tarea de investigación
propuesta se han delimitado diferentes caminos para continuar la actividad.
Dejando de lado algunos caminos, en lo que sigue sólo vamos a considerar
dos de ellos, a los que se puede acceder picando en los títulos
correspondientes. Por un lado, se retoman Relaciones
ya estudiadas y, por otro, se consideran Relaciones
de dualidad en el mundo de los poliedros regulares.
regresar arriba
|

Subapartado
de:
|

