Texto anexo al apartado de Características numéricas. Relaciones
Relaciones de dualidad
En este camino de actividad vamos a considerar las relaciones de dualidad en el mundo de los poliedros regulares para desarrollar actividad.
Para los pares de poliedros regulares que son duales se asocian los enunciados que se han expresado a partir de la tabla de las características numéricas de los poliedros regulares. Éstos implicaban al cubo y al octaedro, al dodecaedro e icosaedro y al tetraedro consigo mismo. La actividad se desarrolla como sigue: |
 |
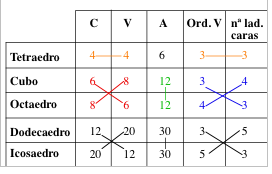
| {1} | P: Vamos a recordar las relaciones que ya teníamos recopiladas en la tabla entre los elementos de los pares de poliedros o de uno consigo mismo. El cubo y el octaedro están relacionados. ¿Qué relaciones podemos establecer entre sus elementos? |
| {2}: | E1: El cubo y el octaedro tienen el mismo número de aristas, 12. |
| {3} | E2: El número de caras del cubo es igual que el número de vértices del octaedro y a la inversa. |
| {4} | E3: En los vértices del cubo se juntan 3 caras y 3 aristas y las caras del octaedro tienen 3 lados y en los vértices del octaedro se juntan 4 caras y 4 aristas y las caras del cubo tienen 4 lados. |
| {5} | P: En el cubo y el octaedro se intercambian el número de caras y de vértices y el número de aristas coincide. También intercambian el número de lados de las caras y el orden de los vértices. ¿Para qué otro par de poliedros podemos construir enunciados análogos? |
| {6} | E1: El dodecaedro y el icosaedro están relacionados igual que el cubo y el octaedro. En la tabla también hay dos cruces y una raya. Yo, hasta que no me aprenda de memoria la frase aún no lo puedo decir rápido. Uno a uno sí, pero todo junto... |
| {7} | E2: El dodecaedro y el icosaedro tienen el mismo número de aristas, 30. Y las caras y los vértices son iguales también. Y lo mismo pasa con las dos últimas columnas. |
| {8} | E3: El número de caras del dodecaedro es igual que el número de vértices del icosaedro y a la inversa. En los vértices del dodecaedro se juntan 3 caras y 3 aristas y las caras del icosaedro tienen 3 lados. Y en los vértices del icosaedro se juntan 5 caras y 5 aristas y las caras del dodecaedro tienen 5 lados. |
| {9}: | P: ¿Qué ocurre con el tetraedro? |
| {10} | E1: El tetraedro está relacionado consigo mismo. El número de caras y de vértices coincide; y también el número de orden de los vértices y el número de lados de sus caras. |
| {11} | P: Vale, en el octaedro y el cubo, el dodecaedro e icosaedro
y el tetraedro consigo mismo se intercambia el número de caras
y de vértices y el número de aristas coincide. Además
el orden de los vértices de uno de ellos es igual al número
de lados del polígono de las caras del otro y a la inversa. |
Casi siempre es necesario centrar la atención sobre el tetraedro ya que al trabajar todo el tiempo con pares de poliedros lo usual es que se den relaciones para los pares y que no se indique lo relativo a un poliedro. Además las sugerencias dadas de que representen visualmente las relaciones y que luego las enuncien verbalmente construyendo enunciados que contengan todos los que implican a un poliedro o pares de poliedros, así como que sustituyan éstos por puntos suspensivos reflejan diferencias para el tetraedro. Mientras que en el cubo y el octaedro, y el dodecaedro e icosaedro en la tabla se reflejan dos cruces y una raya X|X, en el tetraedro no ocurre esto. Además, en el enunciado que recopila todas las relaciones, si bien sí que se indica que las caras se intercambian con los vértices y el orden de los vértices coincide con el número de lados del polígono de las caras, no se apunta lo relativo a las aristas. Sólo al intentar acoplarlo se comprueba que efectivamente podemos incluirlo en el mismo grupo.
Centrar la atención en que tenemos modelos de algunos pares de poliedros inscritos (del tetraedro en el cubo y del cubo en el dodecaedro) puede llevar a sospechar que hay también modelos de pares de poliedros inscrito uno en otro para los pares de poliedros regulares duales. A continuación indicamos cómo se continuó la sesión de clase después de que se hubiera planteado la cuestión ¿Cómo se van a corresponder los elementos de ambos poliedros?
| {12} | P: A ver, el cubo y el octaedro... los vértices y las caras, apoyado en cara y el otro en vértice, o al revés... Por cada vértice hay una cara y cada cara se corresponde con un vértice y las aristas se corresponden una a una [Se apoya en los modelos de la figura]. figura 22 ¿Podeis imaginar un modelo con estos dos poliedros regulares, el cubo y el octaedro, de manera que el octaedro quede inscrito en el cubo? ¿Cómo quedan los elementos del octaedro con respecto a los del cubo? Al igual que hicimos con el tetraedro y el cubo, o el cubo y el dodecaedro, precisar cómo quedan los elementos del cubo, con respecto a los del octaedro. |
| {13}: | E1: Yo creo que los vértices del octaedro estarán en el medio. |
| {14} | E3: Los vértices estarán en el centro de la cara. |
| {15} | E2: Yo creo que el cubo también se puede inscribir en el cubo con los vértices en la cara. Ya me he liado. A ver... Es el cubo el que se queda dentro, igual. Los vértices están en las caras del de fuera. |
En las experimentaciones que hemos realizado, respuestas como la {13}centran la atención en que “el medio” en las caras se llama el “centro” y el de las aristas “el punto medio”. Se incide en que para expresarse con precisión se ha de tener cuidado pues al describir los modelos de pares de poliedros regulares duales, inscrito uno en otro, se habla en repetidas ocasiones tanto del centro de las caras como de punto medio de aristas; y la precisión en el uso del lenguaje geométrico se tiene que ir mejorando progresivamente. La respuesta {15}centra la atención en que se han de distinguir los dos poliedros implicados.
Al igual que se ha sugerido al describir el tetraedro en el cubo y el cubo en el dodecaedro en Puzzles y estructuras rígidas. Relaciones de este mismo apartado, el uso de una tabla facilita expresar las relaciones implicadas entre los elementos de los poliedros que forman los modelos. En la primera columna se indican las características numéricas (caras, vértices y aristas) del poliedro inscrito y en la segunda columna las del circunscrito con las que se corresponden. Y la tabla se puede eliminar pero manteniendo las diferentes posiciones para el poliedro inscrito y circunscrito.
Mostrando los modelos de la figura se confirma las conjeturas que se han hecho al respecto: Se puede introducir tanto el cubo en el octaedro como el octaedro en el cubo. Y también el tetraedro en sí mismo, el dodecaedro en el icosaedro y ya no quedan dudas de que también se puede inscribir el icosaedro en el dodecaedro.
figura 23
Para describir los modelos, por ejemplo el modelo en el que el cubo está inscrito en el octaedro podemos hacerlo de dos maneras: En una de ellas, nos fijamos en los elementos C, V y A del poliedro inscrito (el del interior) e indicamos con qué elementos del poliedro circunscrito (el del exterior) se corresponden. Así, si nos imaginamos como una tabla, o que hay una línea de separación, y en la parte de la izquierda del enunciado se habla de elementos del poliedro inscrito (en este caso el octaedro) y en la parte de la derecha de elementos del poliedro circunscrito (en este caso el cubo), podemos decir:
La otra manera de describir un modelo es fijarse en los elementos de los V y A tanto del poliedro inscrito como del circunscrito y describir con qué elementos se corresponden. En este modelo se cumple:
Y la actividad puede continuar considerando el octaedro inscrito en el cubo u otros pares de poliedros regulares duales: el dodecaedro e icosaedro y el tetraedro consigo mismo. Para ellos se pueden describir los modelos correspondientes.
Llegar a utilizar con precisión el lenguaje geométrico conlleva bastante dificultad; los estudiantes quieren practicar en varias tareas los descubrimientos que se hacen. Además, las tareas si bien a nivel de expresión no introducen apenas variación, y de eso se dan cuenta los estudiantes cuando han comprendido lo que hacen, el aspecto tan diferente de los poliedros implicados hace que la tarea conlleve la dificultad necesaria para que no quede como una tarea repetitiva que lo único que pretende es que se aprendan la frase de memoria.
Además de los modelos de poliedros regulares inscrito uno en otro, para desarrollar actividad matemática se pueden considerar también otros modelos de los pares de poliedros regulares duales. A partir de los modelos de pares de poliedros regulares duales en los que uno queda inscrito en el otro, se pueden imaginar las formas de la figura. Si en el modelo de un poliedro inscrito en su dual se va aumentando el tamaño del poliedro inscrito, las aristas de éste se convierten en aristas paralelas que se van acercando a las aristas del poliedro circunscrito. Llegará un momento en que las aristas se cortarán y se obtendrán los modelos de la figura, que llamamos formas compuestas.
figura 24
Para estos otros modelos de pares de poliedros duales podemos realizar actividades análogas a las ya realizadas con los otros. Dos de ellos se han tratado en el apartado ¨Rompiendo las ideas de cara... Y en Guillén (1991), que se referencia en la sección Para conocer más, se puede encontrar mucha más información sobre la actividad matemática que se puede desarrollar a partir de ellos.
