|
UNIDAD DE MEDIDA |
||
|
La unidad de medida puede ser
dividida en partes |
Relación inversa entre el tamaño de
la unidad y el número de unidades que recubren la superficie |
La unidad de medida debe recubrir
exactamente la superficie |
La
medición es un proceso por medio del cual se asigna un número al área, como
resultado de la comparación de la superficie con otra considerada como unidad.
Por ello es esencial para una adecuada comprensión
de la medida del área, que se posea una buena comprensión del concepto de
unidad de medida. Para ello, se deberá proporcionar al niño las situaciones y
problemas necesarios para que éste conozca y comprenda las propiedades y características de las unidades de medida, que son
las que aquí se muestran.
La
unidad de medida puede ser dividida en partes para facilitar la
medida de una cantidad. Esta propiedad pone de manifiesto el carácter de no
discretitud de la unidad de medida. Esta propiedad la posee, tanto, la unidad
de medida lineal, como la bidimensional.
§ Se trabajará realizando tareas, en las que el niño para calcular el área de una superficie, se vea en la necesidad de fraccionar la unidad de medida con la que está recubriendo la superficie. Ello le permitirá estimar o determinar, mediante una fracción de la unidad de medida, aquellos espacios en los que la unidad de medida entera no cabe.
Tareas
Tarea 1UM (Tarea 29MAurs)
(Tarea 28PNub)
Utiliza un cuadrado como el dado, para medir las áreas de las distintas figuras
y determina el número de unidades
cuadradas que están contenidas en cada una de ellas:
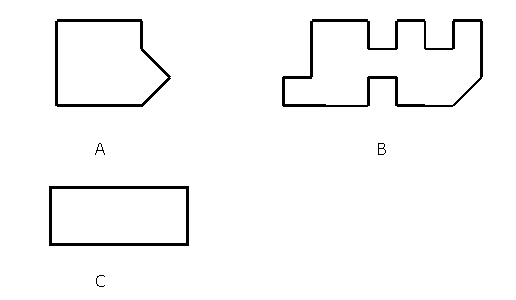
Nota.- Se proporcionará a los alumnos una fotocopia con
la superficie, y varias piezas cuadradas como las indicadas, del material del
que se disponga, para que el niño pueda recubrir la superficie con las unidades
cuadradas.
Objetivos de la tarea:
§
Trabajar las propiedades de la unidad de medida bidimensional: carácter
de no discretitud de la unidad y carácter de recubrimiento de la unidad de
medida.
§
Trabajar el procedimiento numérico de iteración de una unidad de
medida.
§
Trabajar el área como números de unidades que recubren la superficie.
Tarea 2UM (Tarea 9MAurs)
(Tarea 2PNub)
Determina el número de unidades cuadradas
que están contenidas en la figura:
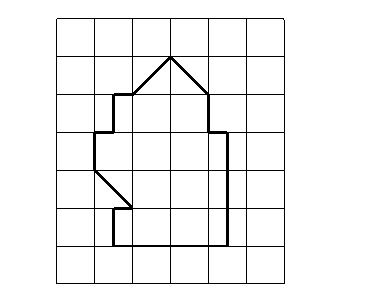
Objetivos de la tarea:
§
Trabajar las propiedades de la unidad de medida bidimensional: Carácter
de recubrimiento de la unidad de medida y carácter de no discretitud de la
unidad.
§
Trabajar el procedimiento numérico de iteración de una unidad de medida
y fracción de ésta.
§
Trabajar el área como números de unidades que recubren la superficie.
(Tarea 3UM) (Tarea 10MAurs) (Tarea 3PNub)
Calcula la medida del área de cada una de las siguientes superficies, utilizando como unidad de medida el cuadrado (A).
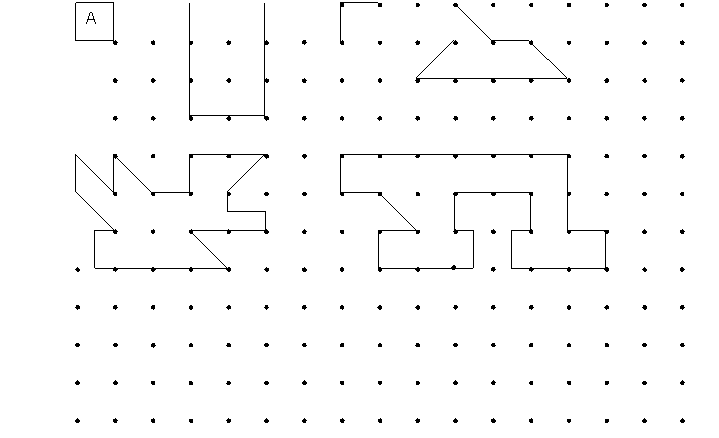
Extraída de Corberán (1996).
Objetivos de la tarea:
§
Trabajar las propiedades de la unidad de medida bidimensional: Carácter
de recubrimiento de la unidad de medida y carácter de no discretitud de la
unidad.
§
Trabajar el procedimiento numérico de descomposición de la figura en
partes iguales.
§
Trabajar el área como números de unidades que recubren la superficie.
¿Te interesa bajarte/imprimir estas actividades y otras
similares para trabajar con tus alumnos? IR A
TAREAS
|
UNIDAD DE MEDIDA |
||
|
La unidad de medida puede ser
dividida en partes |
Relación inversa entre el tamaño de
la unidad y el número de unidades que recubren la superficie |
La unidad de medida debe recubrir
exactamente la superficie |
Existe una relación
inversa entre el tamaño de la unidad y el número de unidades que recubren la
superficie. La comprensión de esta propiedad por parte del alumno le
permitirá admitir que la medida del área de una superficie puede tener asociada
diferentes números procedentes de la medida realizada con unidades de medida
distintas. De este modo se trabaja la disociación del área del número que la
mide, y en consecuencia el área como magnitud
autónoma.
§
Se
trabajará realizando tareas de medida del área de una misma superficie, con el
uso de diferentes unidades de medida entre las que las que se pueda establecer
una relación, de modo que el alumno, compruebe que a mayor tamaño de la unidad
de medida, menor es el número asociado a la medida del área, y viceversa.
Tareas
Tarea 4UM (Tarea 3Mama) (Tarea 7MAurs)
(Tarea 12PNub)
a)
Mide el área de la superficie (S), utilizando las
unidades A, B, C y D. Completa la tabla siguiente:
|
|
Medida del área de
(S) |
|
unidad “A” |
|
|
unidad “B” |
|
|
unidad “C” |
|
|
unidad “C” |
|
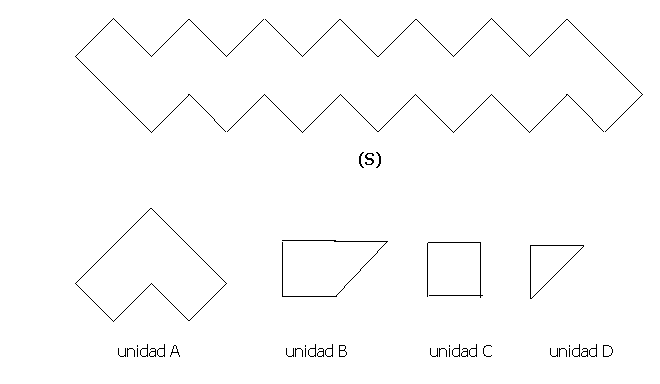
b) Completa la tabla:
|
|
Unidades |
|||
|
A |
B |
C |
D |
|
|
Objeto geométrico |
|
|
|
|
|
A |
|
|
|
|
|
B |
|
|
|
|
|
C |
|
|
|
|
|
D |
|
|
|
|
Nota.- Los alumnos dispondrán de una fotocopia de la superficie (S) y un juego con varias unidades A, B, C y D, del material que se pueda disponer: cartulina, plástico, ...
Extraída de Peterson (1973)
Objetivos de la tarea:
§
Trabajar la disociación del área del número que la mide.
§
Trabajar el área como número de unidades que recubren la
superficie.
§
Trabajar las propiedades de la unidad de medida de área
bidimensional: i) Carácter de recubrimiento de la unidad de medida; ii)
Relación inversa entre el número de unidades que recubren la superficie y el
tamaño de la unidad; iii) Carácter de no discretitud de la unidad.
§
Trabajar procedimientos numéricos con uso de una unidad
bidimensional.
Tarea 5UM (Tarea 14Mama) (Tarea 24MAurs)
(Tarea 24PNub)
Hugo debe realizar un mosaico para un
trabajo del colegio. La superficie que debe recubrir es la que se muestra en la
figura.
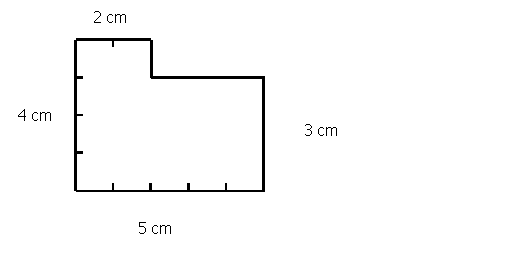
a) ¿Cuántas baldosas como
½ cm
b)
¿Cuántas baldosas como
½ cm
Si
Hugo no tiene mucho tiempo para realizar el trabajo, ¿cuál de las dos baldosas
elegirá para realizar el mosaico?
Adaptada de Corberán (1996)
Objetivos de la tarea:
§
Trabajar las
propiedades de la unidad de medida de área bidimensional: i) Carácter de
recubrimiento de la unidad de medida; ii) Relación inversa entre el número de
unidades que recubren la superficie y el tamaño de la unidad.
§
Trabajar la disociación del área del número que la mide.
§
Trabajar el área como número de unidades que recubren la
superficie.
§
Trabajar procedimientos numéricos con uso de una unidad
bidimensional.
¿Te interesa bajarte/imprimir estas actividades y otras
similares para trabajar con tus alumnos? IR A
TAREAS
|
UNIDAD DE MEDIDA |
||
|
La unidad de medida puede ser
dividida en partes |
Relación inversa entre el tamaño de
la unidad y el número de unidades que recubren la superficie |
La unidad de medida debe recubrir
exactamente la superficie |
Es esencial
que el alumno comprenda que la unidad debe recubrir
exactamente la superficie. Esta propiedad determina las características
que debe poseer una buena unidad de
medida: debe ser fácilmente reproducible, fácilmente divisible y no debe dejar
huecos en el momento de recubrir la superficie con unidades o sus
fracciones. Estas condiciones deben conducir a una elección racional del
cuadrado como la unidad de área bidimensional más “conveniente”. Esta propiedad
se refiere sólo a unidades de medida bidimensional.
§
Se
trabajará realizando tareas de medida del área de una misma superficie, con el
uso de diferentes unidades de medida, de modo que el alumno pueda valorar con
cual de ellas le ha resultado más fácil, dificultoso e incluso imposible
realizar el recubrimiento de la superficie.
Tareas
Tarea 6UM (Tarea 25MAurs)
(Tarea 25PNub)
¿Cuántas
formas (unidades) como
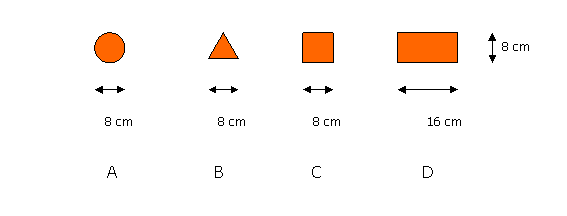
Nota.- A los alumnos se
les proporcionará cada una figura en una hoja diferente, así como un juego con
las diferentes formas, A, B, C y D, con el fin de que las reproduzcan sobre la
figura conforme las van iterando.
Objetivos de la tarea:
§
Trabajar las propiedades de la unidad de medida de área
bidimensional: carácter de recubrimiento de la unidad de medida.
§
Trabajar las características que debe poseer una buena
unidad de medida: debe ser fácilmente reproducible, fácilmente divisible y no
debe dejar huecos.
§
Romper con la tendencia, muy extendida entre los
estudiantes, de ligar la elección de las unidades de medida a la forma de la
superficie, a partir del estudio de las características de una buena unidad de
medida. Se irá trabajando, de ese modo, la elección racional de la unidad
cuadrada.
- Trabajar
el área como número de unidades que recubren la superficie.
- Trabajar
procedimientos numéricos con uso de una unidad bidimensional.
¿Te interesa bajarte/imprimir estas actividades y otras similares
para trabajar con tus alumnos? IR A TAREAS