Tarea 3MAcp
(Tarea 5MAma) (Tarea 16PG)
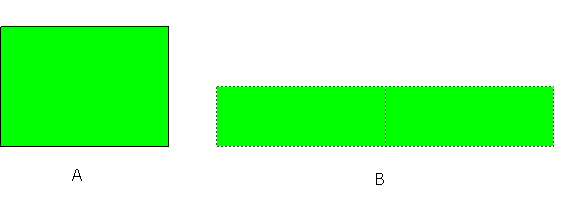
Imagínate que estas figuras representan dos campos cubiertos de hierba.
¿Tiene el campo A la misma cantidad de hierba que el campo B?
Nota.- Se proporcionará al alumno
rectángulos iguales a los que constituyen la figura B.
Extraída de Hughes, Bell & Rogers (1975)
Objetivos de la tarea:
§
Trabajar
el área como cantidad de plano ocupado por la superficie.
§
Trabajar
la disociación entre el área y la forma de la superficie.
§
Trabajar
la conservación de área.
§
Romper
con la creencia muy extendida en los niños, que una figura más larga tiene
mayor área, al fijarse en una única dimensión.
§
Trabajar
los procedimientos geométricos de: i) Comparación indirecta por recorte y
pegado de las piezas en las que queda descompuesta la superficie. ii)
Reconfiguración por complementariedad de formas de las partes en las que se ha
dividido la superficie.
Tarea 4MAcp (Tarea 6MAma)
(Tarea 17PG)
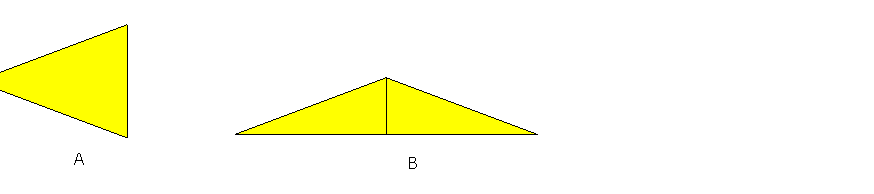
Si tuvieras que pintar la figura A, ¿necesitarías la misma o diferente
cantidad de pintura que para pintar la figura B?
Extraída de Hughes, Bell & Rogers (1975)
Objetivos de la tarea:
§
Trabajar
el área como cantidad de plano ocupado por la superficie.
§
Trabajar
la disociación entre el área y la forma de la superficie.
§
Trabajar
la conservación de área.
§
Trabajar
los procedimientos geométricos de: Descomposición conveniente de la superficie
con posterior reconfiguración por complementariedad de formas de las partes en
las que se ha dividido la superficie.
Tarea 4MAma (Tarea 13MAurs)
(Tarea 16PNub) (Tarea 9UM)
Calcula cuántas figuras A caben en la
figura (S), cuántas figuras B caben en la figura (S) y cuántas figuras C caben
en la figura (S). Completa la tabla siguiente:
|
|
Figura A (unidad A) |
Figura B (unidad B) |
Figura C (unidad C) |
|
Superficie (S) |
|
|
|
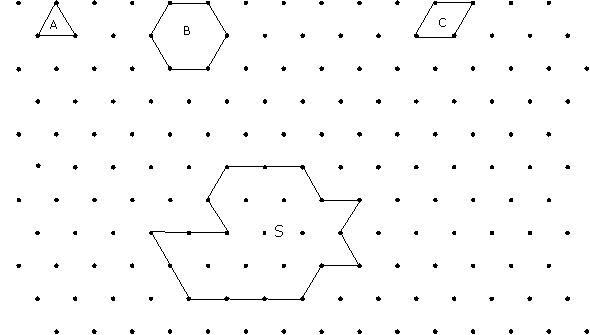
Extraída de Musser
& Burger
(1988)
Objetivos de la tarea:
§
Trabajar
la disociación del área y del número que la mide.
§
Trabajar
el área como número de unidades que recubren la superficie.
§
Trabajar
las propiedades de la unidad de medida de área bidimensional: i) Carácter de
recubrimiento de la unidad de medida; ii) Relación inversa entre el número de
unidades que recubren la superficie y el tamaño de la unidad; iii) Carácter de
no discretitud de la unidad.
§
Trabajar
procedimientos numéricos con uso de una unidad bidimensional.
Tarea 4MAurs (Tarea 17PNub)
¿Cuántos cuadrados como el A, se
necesitan para formar la siguientes figuras?
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
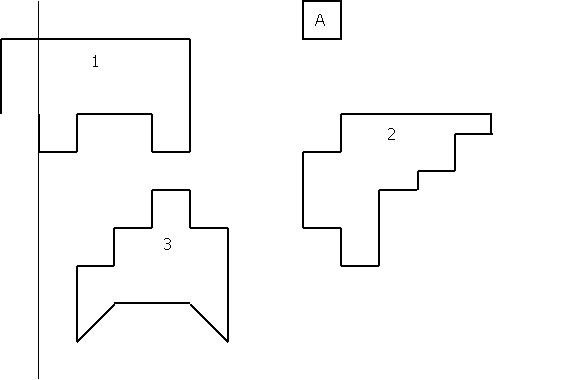
Objetivos de la tarea:
- Trabajar el área como número de unidades que recubren la
superficie.
- Trabajar procedimientos numéricos con uso de unidad de medida
bidimensional.
Tarea 5MAurs (Tarea 18PNub)
¿Cuántas veces cabe la figura A en cada una de las figuras 1, 2 y 3?

Extraída
de Corberán (1996)
Objetivos de la tarea:
§ Trabajar el área como número de unidades que recubren la superficie.
§ Trabajar procedimientos numéricos con uso de una unidad de medida bidimensional.
Tarea 4MApd (Tarea 13PNuu)
(Tarea 9A-P)
Determina el área y el perímetro de cada figura geométrica que se muestra a continuación y completa la tabla siguiente:
|
Figura |
Área |
Perímetro |
|
A |
|
|
|
B |
|
|
|
C |
|
|
|
D |
|
|
¿Qué puedes decir sobre los perímetros? ¿Qué puedes decir sobre las áreas?
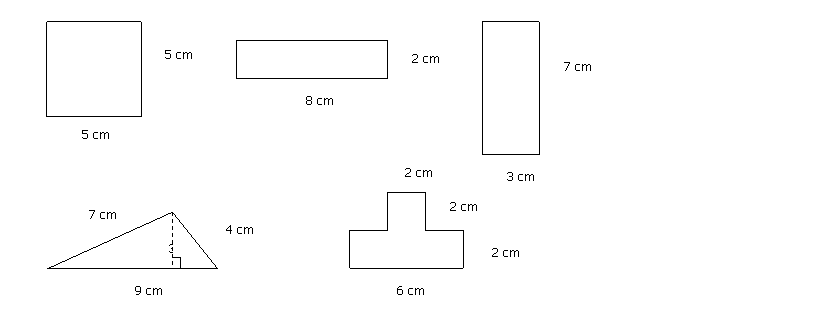
Objetivos de la tarea:
§ Trabajar el área como producto de dos dimensiones lineales.
§ Trabajar procedimientos numéricos con uso de unidad unidimensional.
§ Trabajar la disociación del área del perímetro de la superficie.
Tarea 7PG (Tarea 12MAcp)
(Tarea 10A-P)
La figura (A) ha sido cortada en 2 piezas que han sido reorganizadas
–sin superponerse- para construir la figura (B).
a) Compara sus áreas. ¿Tienen igual área?
b) Compara sus perímetros. ¿Tiene igual perímetro?

Extraída de Corberán (1996)
Objetivos de la tarea:
§
Trabajar el procedimiento
geométrico de reconfiguración por complementariedad de las formas en las que se
ha dividido la superficie. Se establece una relación de igualdad entre las
superficies.
§
Trabajar la disociación del área
del perímetro.
§
Trabajar la conservación del área.
§
Trabajar el área como cantidad de
plano ocupado por la superficie.
Tarea 8PG
(Tarea 13MAcp)
a) ¿Qué fracción del cuadrado representa la zona azul?

b) ¿Qué fracción del cuadrado representa la zona roja?

c) ¿Qué fracción del cuadrado representa la zona verde?

Objetivos de la tarea:
§
Trabajar el procedimiento
geométrico de descomposición conveniente de la superficie en partes. Mediante
el uso de una fracción se establece la relación de la parte respecto del todo.
Se establece una relación numérica entre las áreas.
§
Trabajar el área como cantidad de
plano ocupado por la superficie.
Tarea 9PG (Tarea 14MAcp)
¿Qué fracción del triángulo representa la zona sombreada?

Objetivos de la tarea:
§
Trabajar el procedimiento
geométrico de descomposición conveniente de la superficie en partes iguales. Mediante
el uso de una fracción se establece la relación de la parte respecto del todo.
Se establece una relación numérica entre las áreas.
§
Trabajar el área como cantidad de
plano ocupado por la superficie.
Tarea 10PG (Tarea 15MAcp)
¿Qué fracción de la figura representa la zona verde?
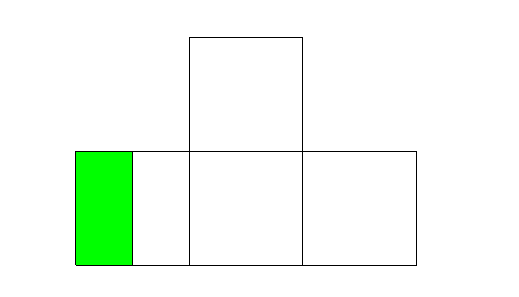
Objetivos de la tarea:
§
Trabajar el procedimiento geométrico
de descomposición conveniente de la superficie en partes iguales. Mediante el
uso de una fracción se establece la relación de la parte respecto del todo. Se
establece una relación numérica entre las áreas.
§
Trabajar el área como cantidad de
plano ocupado por la superficie.
Tarea 6PNub (Tarea 9MAma)
(Tarea 14MAurs)
¿Cuántas figuras (A) caben en cada una de las siguientes figuras? ¿Existen figuras que posean la misma área?
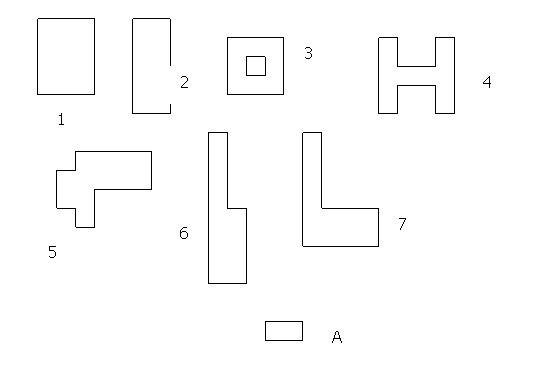
Nota.- A los alumnos se les proporcionará una fotocopia con cada una de las figuras (1), (2), (3), (4), (5), (6), (7) y (8) y una pieza de cartulina como la figura (A).
Adaptada de Hughes, Bell & Rogers (1975).
Objetivos de la tarea:
§ Trabajar el procedimiento numérico de iteración de la unidad de medida.
§
Trabajar el área como números de unidades que
recubren la superficie.
§
Trabajar
la disociación del área de la forma de la superficie.
§
Trabajar
la conservación del área.
Tarea 7PNub
(Tarea 18PG) (Tarea 15MAurs)
Encuentra
el área del polígono:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
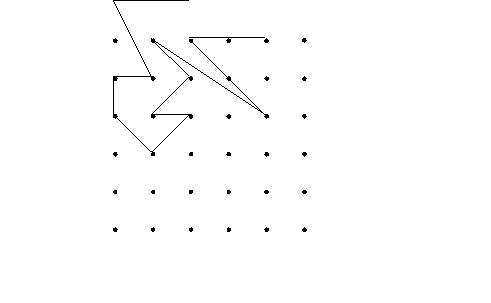
Extraído de Corberán et alii (1989).
Objetivos de la tarea:
§ Trabajar la combinación de un procedimiento geométrico con uno numérico. El primero será utilizado con objeto de facilitar el cálculo del número de unidades que recubren exactamente la superficie. El segundo para determinar la medida del área.
§ Trabajar el procedimiento geométrico de descomposición conveniente de la superficie con posterior reconfiguración por complementariedad de formas.
§
Trabajar
el procedimiento numérico de iteración de una unidad de medida.
§
Trabajar
el área como números de unidades que recubren la superficie.
Tarea 8PNub
(Tarea 16MAurs)
Determina el número de unidades cuadradas contenidas en la figura:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
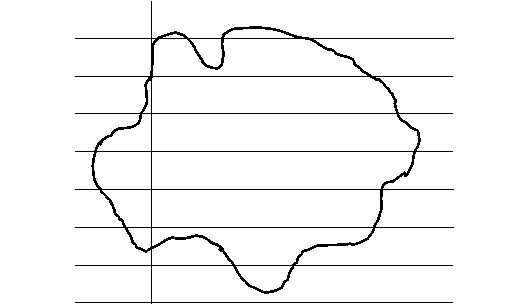
Objetivos de la tarea:
§
Trabajar
el procedimiento numérico de iteración de una unidad de medida y fracción de
ésta, para estimar la medida del área de una superficie no poligonal.
§
Trabajar
la idea de mejora de la medida, realizando aproximaciones sucesivas desde el
interior de la superficie, considerando tramas cuadriculadas, cuyos cuadrados
sean fracciones sucesivas del cuadrado de la trama original.
§
Trabajar,
si se desea, la medida del área, a partir de aproximaciones sucesivas desde
interior y exterior de la superficie, comprobando que la medida del área es un
número mayor que el número de unidades cuadradas contenidas en la superficie, y
menor que el número de unidades cuadradas contenidas y que contienen a la
superficie.
§
Trabajar
el área como números de unidades que recubren la superficie.
Tarea 9PNub
(Tarea 17MAurs) (Tarea 19PG)
Calcula el número de unidades cuadradas que recubren el triángulo de la figura:
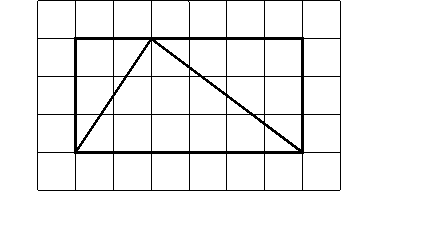
Objetivos de la tarea:
§ Trabajar la combinación de un procedimiento geométrico con uno numérico. El primero será utilizado con objeto de facilitar el cálculo del número de unidades que recubren exactamente la superficie. El segundo para determinar la medida del área.
§ Trabajar el procedimiento geométrico de descomposición conveniente de la superficie.
§ Trabajar el procedimiento numérico de iteración de una unidad de medida.
§
Trabajar
el área como números de unidades que recubren la superficie.
§
Trabajar
el área de un triángulo como la mitad del área del rectángulo de igual base y
altura que lo contiene.
Tarea 10PNub
(Tarea 18MAurs) (Tarea 20PG)
Calcula el área del cuadrilátero:
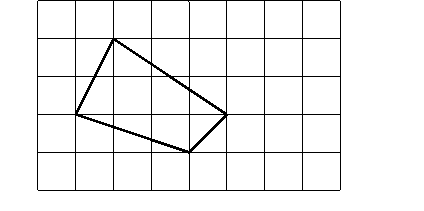
Extraída de Corberán (1996)
Objetivos de la tarea:
§ Trabajar la combinación de un procedimiento geométrico con uno numérico. El primero será utilizado con objeto de facilitar el cálculo del número de unidades que recubren exactamente la superficie. El segundo para determinar la medida del área.
§ Trabajar el procedimiento geométrico de descomposición conveniente de la superficie.
§ Trabajar el procedimiento numérico de iteración de una unidad de medida.
§
Trabajar
el área como números de unidades que recubren la superficie.
§
Trabajar el área de un triángulo como la
mitad del área del rectángulo de igual base y altura que lo contiene.
Tarea 7PNuu
(Tarea 22MAurs) (Tarea 22PNub)
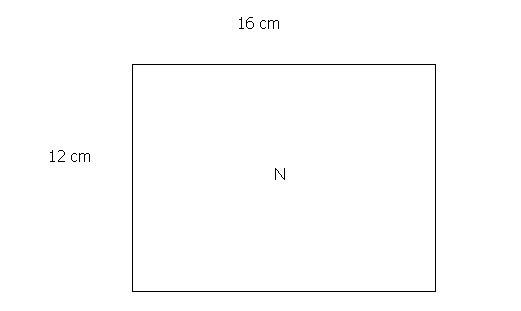
Si se necesitan 4 formas rectangulares
M, para cubrir N, ¿cuál debería ser la altura y anchura de la figura M?
Extraída de Leutzinger & Nelson (1980)
Objetivos de la tarea:
§
Familiarizar
a los alumnos con la relación de la medida del área de una figura y las medidas
de sus dimensiones, a partir de la iteración de una unidad de medida, que
estará condicionada por la longitud de cada una de las dimensiones de la
figura.
§
Trabajar
el área como números de unidades que recubren la superficie.
§
Trabajar
la disociación del área de la forma de la superficie.
§
Trabajar
la disociación del área del perímetro de la superficie.
Tarea 8PNuu
(Tarea 8MApd) (Tarea 23PG)
Transforma el rombo siguiente en un rectángulo que tenga igual área. Calcula el área rombo.
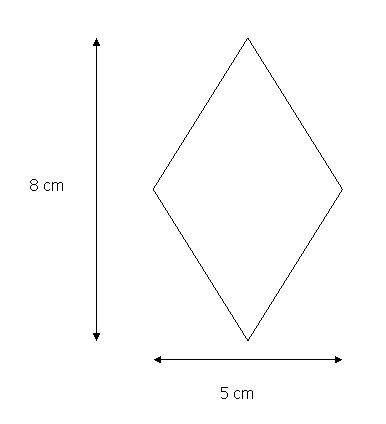
Objetivos de la tarea:
§ Trabajar la combinación de un procedimiento geométrico con uno numérico. El primero será utilizado con objeto de facilitar el cálculo del área. El segundo para determinar la medida del área.
§ Trabajar el procedimiento geométrico de descomposición conveniente de la superficie con posterior reconfiguración por complementariedad de formas.
§ Trabajar el procedimiento numérico: uso de la fórmula para el cálculo del área del rectángulo, que requiere del uso de una unidad de medida unidimensional.
§ Trabajar el área como producto de dos dimensiones lineales.
§ Trabajar el área del rombo como el área de un rectángulo.
Tarea 9PNuu
(Tarea 9MApd) (Tarea 24PG)
Transforma el trapecio siguiente en un rectángulo que tenga igual área. Calcula el área trapecio.
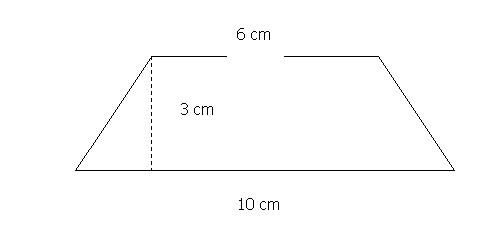
Objetivos de la tarea:
§ Trabajar la combinación de un procedimiento geométrico con uno numérico. El primero será utilizado con objeto de facilitar el cálculo del área. El segundo para determinar la medida del área.
§ Trabajar el procedimiento geométrico de descomposición conveniente de la superficie con posterior reconfiguración por complementariedad de formas.
§ Trabajar el procedimiento numérico: uso de la fórmula para el cálculo del área del rectángulo, que requiere del uso de una unidad de medida unidimensional.
§ Trabajar el área como producto de dos dimensiones lineales.
§ Trabajar el área del trapecio como el área de un rectángulo.
Tarea 7UM
(Tarea 26MAurs) (Tarea 26PNub)
Calcula el área de las superficies (A), (B) y (C), utilizando para ello y en cada caso la unidad que consideres más apropiada de las dadas (1), (2) y (3).
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
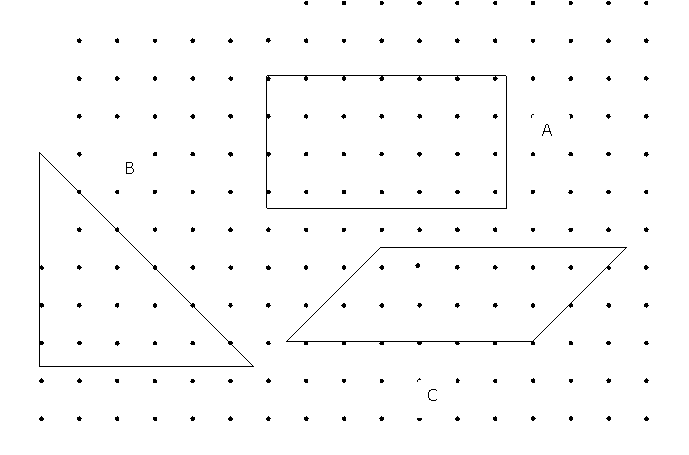
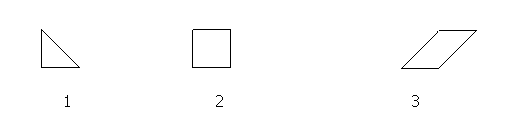
Extraída de Corberán (1996)
Objetivos de la tarea:
§
Trabajar
las propiedades de la unidad de medida de área bidimensional: carácter de
recubrimiento y r de no discretitud de la unidad de medida.
§
Trabajar
las características que debe poseer una buena unidad de medida: debe ser
fácilmente reproducible, fácilmente divisible y no debe dejar huecos.
§
Romper
con la tendencia, muy extendida entre los estudiantes, de ligar la elección de
las unidades de medida a la forma de la superficie, a partir del estudio de las
características de una buena unidad de medida. Se irá trabajando, de ese modo,
la elección racional de la unidad cuadrada.
- Trabajar el área como número de
unidades que recubren la superficie.
- Trabajar procedimientos
numéricos con uso de una unidad bidimensional.
Tarea 11A-P (Tarea 19MAcp)
El hexágono (B) se ha obtenido presionando hacia dentro uno de los
vértices del hexágono (A), tal y como se indica en la figura. ¿Tienen el mismo
perímetro? ¿Tienen la misma área?
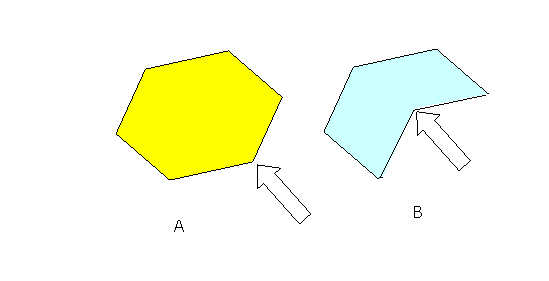
Objetivos de la tarea:
§ Trabajar el hecho de que la transformación de la superficie a partir de la presión sobre uno de los vértices, conserva el perímetro y no el área.
§ Trabajar el área como cantidad de plano contenido en la superficie.
Tarea 12A-P (Tarea 30MAurs) (Tarea 29PNub)
Completa la tabla siguiente:
|
|
Medida del área |
Medida del perímetro |
|
Figura A |
|
|
|
Figura B |
|
|
|
Figura C |
|
|
|
Figura D |
|
|
Toma como unidad de área el cuadrado
(S), y como unidad de longitud (L).
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
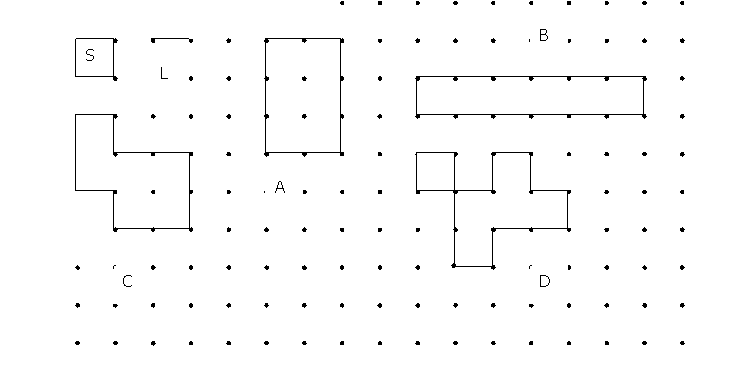
Extraída de Corberán (1996)
Objetivos de la tarea:
§ Trabajar el hecho de que superficies de igual área poseen diferente perímetro.
§ Trabajar el área como número de unidades que recubren exactamente la superficie.
§
Trabajar el procedimiento numérico
de descomposición de la figura en partes iguales.