|
PROCEDIMIENTOS PARA COMPARAR Y MEDIR ÁREAS |
|
|
PROCEDIMIENTOS DE CARÁCTER GEOMÉTRICO |
PROCEDIMIENTOS DE CARÁCTER NUMÉRICO |
Los procedimientos de naturaleza geométrica son aquellos que utilizan métodos
puramente geométricos donde el número está ausente de cualquier razonamiento.
El objetivo no es cuantificar el área sino comparar áreas de superficies para
establecer entre ellas relaciones de igualdad o inclusión, pudiendo en
determinadas situaciones concretar el tipo de relación, como por ejemplo: que
un área es el triple de la otra. Este tipo de estudio conduce a un tratamiento cualitativo del área.
Los procedimientos geométricos facilitan la comprensión de la conservación del área de una superficie, que juega un papel esencial en el aprendizaje significativo del área, y colaboran en la disociación del área de la forma y del perímetro de la superficie, y de ese modo se trabaja el área como magnitud autónoma y se trabaja evitar la confusión entre el área y el perímetro.
Algunos procedimientos geométricos: estimación; superposición; recorte y pegado; descomposición conveniente de la superficie; reconfiguración por complementariedad de formas de las partes en la que se ha dividido la superficie; descomposición conveniente de la superficie con posterior reconfiguración por complementariedad de formas.
Tareas
Tarea 1PG (Tarea 6MAcp)
Compara estos dos estanques. ¿En cuál de los dos estanques hay más
espacio para que los patos paseen por él?
Adaptada de Corberán (1996).
Objetivos
de la tarea:
§ Trabajar el procedimiento geométrico de comparación indirecta, ya que para comparar las dos superficies es necesario “partir” el estanque (A) en “trozos” para poder superponerlos sobre el (B), y así poder emitir un juicio. Se establece una relación de menor/mayor entre las superficies.
§
Trabajar el área como cantidad de
plano ocupado por la superficie.
Tarea 2PG (Tarea 7MAcp) (Tarea 11MAma) (Tarea 6A-P)
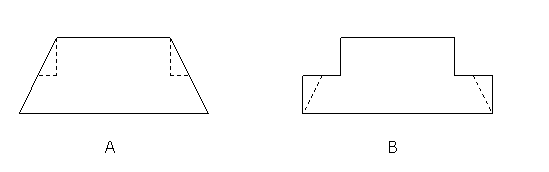
La figura (A) ha sido cortada en 3 piezas que han sido reorganizadas
–sin superponerse- para construir la figura (B).
a)
Compara
el área de la figura (A) con la de (B). ¿Son iguales?
b) Compara los perímetros de las dos
figuras. ¿Son iguales?
Extraída de Corberán (1996).
Objetivos de la tarea:
§
Trabajar el procedimiento
geométrico de reconfiguración por complementariedad
de las formas en las que se ha dividido la superficie. Se establece una
relación de igualdad entre las superficies.
§
Trabajar la “relación” área-perímetro:
superficies de igual área poseen diferente perímetro.
§
Trabajar la conservación del área.
§
Trabajar
el área como cantidad de plano ocupado por la superficie.
§
Trabajar
la disociación entre el área y la forma de la superficie.
Tarea 3PG (Tarea 8MAcp)
(Tarea 12MAma) (Tarea 7A-P)
¿Ocupan estas dos superficies la misma cantidad de plano o diferente?
Extraída de Hughes
(1979).
Objetivos de la tarea:
§
Trabajar el procedimiento
geométrico de reconfiguración por complementariedad
de las formas en las que se ha dividido la superficie. Se establece una
relación de igualdad entre las superficies.
§
Trabajar la conservación del área.
§
Trabajar la “relación”
área-perímetro: superficies de igual área poseen diferente perímetro.
§
Trabajar el área como cantidad de
plano ocupado por la superficie.
§
Trabajar
la disociación entre el área y la forma de la superficie.
Tarea 4PG
(Tarea 9MAcp) (Tarea 13MAma)
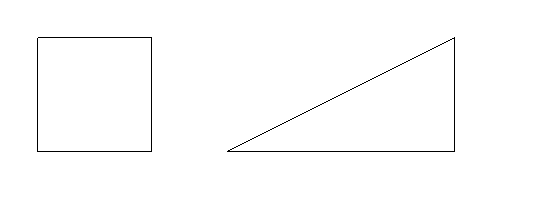
Imagínate que estos son dos pasteles
y tu tienes mucha hambre, ¿cuál preferirías tener? ¿Por qué dices eso?
Extraída de Hughes,
Objetivos de la tarea:
§
Trabajar el procedimiento
geométrico de descomposición conveniente de la superficie con posterior reconfiguración por complementariedad de las formas en las
que se ha dividido la superficie. Se establece una relación de igualdad entre
las superficies.
§
Trabajar la conservación del área.
§
Trabajar el área como cantidad de
plano ocupado por la superficie
§
Trabajar la disociación entre el área y la
forma de la superficie.
Tarea 5PG
(Tarea 10MAcp)
¿Qué relación existe entre el área de la zona amarilla y el área del cuadrado?
Adaptada
de Castelnuovo (1981)
Objetivos de la tarea:
§
Trabajar el procedimiento
geométrico de descomposición conveniente de la superficie con posterior reconfiguración por complementariedad de las formas en las
que se ha dividido la superficie. Se establece una relación numérica entre las
superficies.
§
Trabajar el área como cantidad de
plano ocupado por la superficie.
Tarea 6PG
(Tarea 11MAcp)
¿Qué fracción de la parte interior del cuadrado de la figura representa la:
a) zona azul? b) zona rosa? c) zona amarilla? d) zona verde?
Extraída de Hoffer
(1979).
Objetivos de la tarea:
§
Trabajar el procedimiento
geométrico de descomposición conveniente de la superficie en partes iguales. Mediante
el uso de una fracción se establece la relación de la parte respecto del todo.
Se establece una relación numérica entre las áreas.
§
Trabajar el área como cantidad de
plano ocupado por la superficie.
¿Te
interesa bajarte/imprimir estas actividades y otras similares para trabajar con
tus alumnos? IR A TAREAS
|
PROCEDIMIENTOS PARA COMPARAR Y MEDIR ÁREAS |
|
|
PROCEDIMIENTOS DE CARÁCTER GEOMÉTRICO |
PROCEDIMIENTOS DE CARÁCTER NUMÉRICO |
Los procedimientos de naturaleza numérica tiene por objeto cuantificar el área, bien
sea para comparar áreas de superficies o bien para determinar la medida del
área de una superficie. El uso de este tipo de procedimientos conduce a un tratamiento cuantitativo del área.
Los procedimientos de esta naturaleza requieren previamente a su utilización de la elección de una unidad de medida. Es esencial considerar el carácter bidimensional o unidimensional de la unidad de medida requerida, para determinar el momento y orden en el que hay que presentárselos a los alumnos. Los alumnos deberán familiarizarse en primer lugar con los procedimientos numéricos que utilizan una unidad de carácter bidimensional.
Procedimientos
numéricos que requieren una unidad de medida bidimensional: i) Iteración de una unidad de
medida; ii) Descomposición de la superficie en partes
iguales; iii) Aproximaciones sucesivas desde el
interior y el exterior de la superficie.
El número resulta de una operación aditiva, que procede del recuento de unidades o fracción de ésta que recubre exactamente la superficie.
Procedimientos
numéricos que requieren una unidad de medida unidimensional: uso de fórmulas
El número resulta de una operación multiplicativa, que resulta del producto
de dos unidades unidimensionales.
Tareas
Tarea 1PNub (Tarea 8MAurs) (Tarea 8UM)
Utiliza las piezas (A) (B) y (C) para medir las áreas de las figuras
(1), (2) y (3). ¿Cuál de todas ellas es la que posee mayor área? ¿y la que posee menor área?
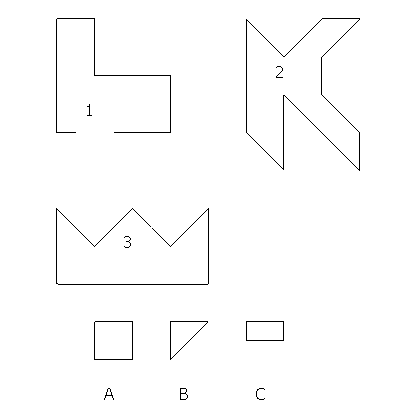
Nota.- Proporcionar a los alumnos una fotocopia con cada una de las
figuras (1), (2) y (3), así como varias piezas de las formas (A), (B) y (C).
Adaptada de Corberán (1996)
Objetivos de la tarea:
§
Trabajar
el procedimiento numérico de iteración de una unidad de medida.
§
Trabajar
las propiedades de la unidad de medida bidimensional: i) Carácter de
recubrimiento de la unidad de medida; ii) Relación
inversa entre el número de unidades que recubren la superficie y el tamaño de
la unidad; iii) Carácter de no discretitud
de la unidad.
§
Trabajar
el área como números de unidades que recubren la superficie.
Tarea 2PNub (Tarea 9MAurs) (Tarea 2UM)
Determina el número de unidades cuadradas que están contenidas en la
figura:
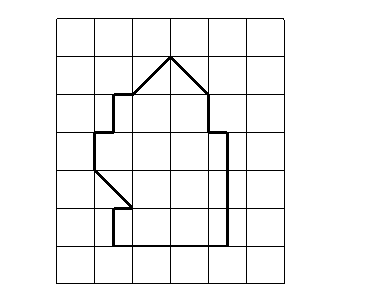
Objetivos de la tarea:
§
Trabajar
el procedimiento numérico de iteración de una unidad de medida y fracción de
ésta.
§
Trabajar
las propiedades de la unidad de medida bidimensional: Carácter de recubrimiento
de la unidad de medida y carácter de no discretitud
de la unidad.
§
Trabajar
el área como números de unidades que recubren la superficie.
Tarea 3PNub (Tarea 10MAurs) (Tarea 3UM)
Calcula la medida del área de cada una de las siguientes superficies, utilizando como unidad de medida el cuadrado (A).
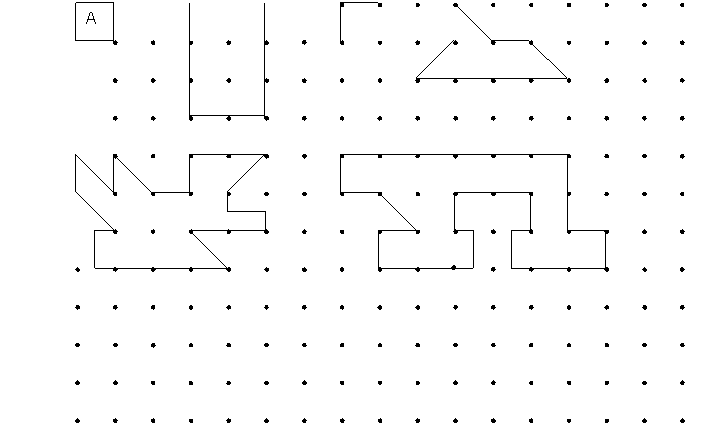
Extraída de Corberán (1996).
Objetivos de la tarea:
§
Trabajar
el procedimiento numérico de descomposición de la figura en partes iguales.
§
Trabajar
las propiedades de la unidad de medida bidimensional: Carácter de recubrimiento
de la unidad de medida y carácter de no discretitud
de la unidad.
§
Trabajar
el área como números de unidades que recubren la superficie.
Tarea 4PNub (Tarea 11MAurs) (Tarea14PG)
Encuentra
el área del polígono:
Extraído de Corberán et alii (1989).
Objetivos de la tarea:
§ Trabajar la combinación de un procedimiento geométrico con uno numérico. El primero será utilizado con objeto de conseguir una figura de igual área que la dada, en la que el cálculo del número de unidades que recubren exactamente la superficie sea mucho más sencillo. El segundo será utilizado para determinar la medida del área.
§ Trabajar el procedimiento geométrico de descomposición conveniente de la superficie con posterior reconfiguración por complementariedad de formas. Se muestra el inicio del proceso de transformación de la superficie dada en un cuadrado.
§
Trabajar
el procedimiento numérico de iteración de una unidad de medida.
§
Trabajar
el área como números de unidades que recubren la superficie.
Tarea 5PNub (Tarea 12MAurs) (Tarea 15PG)
Encuentra
el área del polígono:
Extraído de Padilla (1990).
Objetivos de la tarea:
§ Trabajar la combinación de un procedimiento geométrico con uno numérico. El primero será utilizado con objeto de conseguir una figura de igual área que la dada, en la que el cálculo del número de unidades que recubren exactamente la superficie sea mucho más sencillo. El segundo para determinar la medida del área.
§ Trabajar el procedimiento geométrico de descomposición conveniente de la superficie con posterior reconfiguración por complementariedad de formas.
§
Trabajar
el procedimiento numérico de iteración de una unidad de medida.
§
Trabajar
el área como números de unidades que recubren la superficie.
Tarea 1PNuu (Tarea 19MAurs) (Tarea 19PNub)
Observa las siguientes figuras:
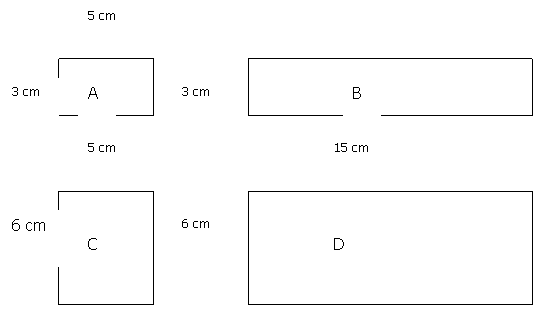
a)
¿Cuántas
figuras A se necesitan para cubrir la figura B?
b)
¿Cuántas
figuras A se necesitan para cubrir la figura C?
c)
¿Cuántas
figuras A se necesitan para cubrir la figura D?
d)
¿Cuántas
figuras B se necesitan para cubrir la figura D?
e)
¿Cuántas
figuras C se necesitan para cubrir la figura D?
f)
¿Cómo
es el área de la figura B comparándola con la de la figura C?
Extraída de Leutzinger & Nelson (1980)
Objetivos de la tarea:
§
Familiarizar
a los alumnos con la relación de la medida del área de una figura y las medidas
de sus dimensiones, a partir de la iteración de una unidad de medida, que
estará condicionada por la longitud de cada una de las dimensiones de la
figura.
§
Trabajar
el área como números de unidades que recubren la superficie.
§
Colaborar
en romper la tendencia de los niños de emitir un juicio sobre el área de dos
figuras, observando sólo una de sus dimensiones.
Tarea 2PNuu (Tarea 20MAurs) (Tarea 20PNub)
a) La figura F tiene un área 4 veces
la de la figura A, ¿cuál debería ser la longitud de F?
b) La figura G tiene un área 6 veces
la de la figura C. ¿Cuál debería ser la longitud de la figura G?
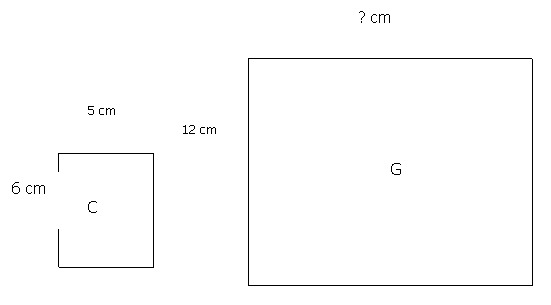
Extraída de Leutzinger & Nelson (1980)
Objetivos de la tarea:
§
Familiarizar
a los alumnos con la relación de la medida del área de una figura y las medidas
de sus dimensiones, a partir de la iteración de una unidad de medida, que
estará condicionada por la longitud de cada una de las dimensiones de la
figura.
§
Trabajar
el área como números de unidades que recubren la superficie.
§
Colaborar
en romper la tendencia de los niños de emitir un juicio sobre el área de dos
figuras, observando sólo una de sus dimensiones.
Tarea 3PNuu (Tarea 21MAurs) (Tarea 21PNub)
Los padres de Hugo han decidido cambiar el suelo
del comedor de su casa, y para ello han elegido unas baldosas de
Adaptada de Hughes, Bell & Rogers (1975)
Objetivos de la tarea:
§
Familiarizar
a los alumnos con la relación de la medida del área de una figura y las medidas
de sus dimensiones, a partir de la iteración de una unidad de medida, que
estará condicionada por la longitud de cada una de las dimensiones de la
figura.
§
Trabajar
el área como números de unidades que recubren la superficie.
§
Trabajar
el estudio de unidades de longitud.
Tarea 4PNuu (Tarea 5MApd) (Tarea 21PG)
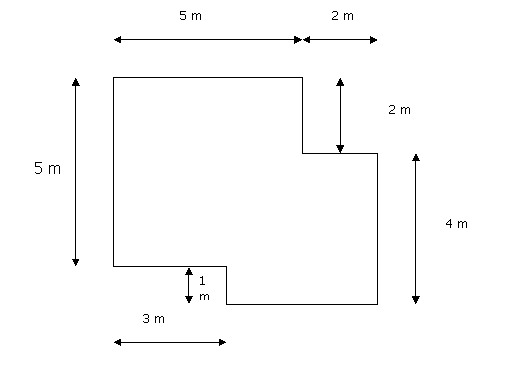
Calcula el área de la zona sombreada.
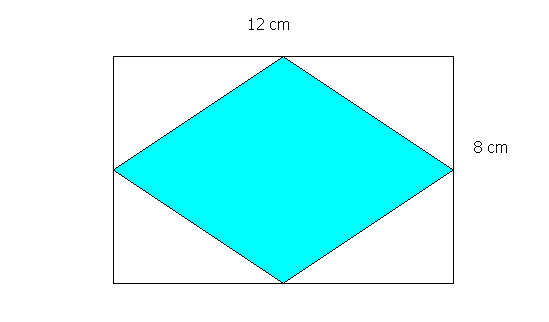
Extraída de Corberán (1996)
Objetivos de la tarea:
§ Trabajar la combinación de un procedimiento geométrico con uno numérico. El primero será utilizado con objeto de facilitar el cálculo del área. El segundo para determinar la medida del área.
§ Trabajar el procedimiento geométrico de descomposición conveniente de la superficie.
§ Trabajar el procedimiento numérico: uso de la fórmula para el cálculo del área del rectángulo, que requiere del uso de una unidad de medida unidimensional.
§ Trabajar el área como producto de dos dimensiones lineales.
Tarea 5PNuu (Tarea 6MApd) (Tarea 22PG)
Transforma el paralelogramo siguiente en un rectángulo que tenga igual área. Calcula el área del paralelogramo.
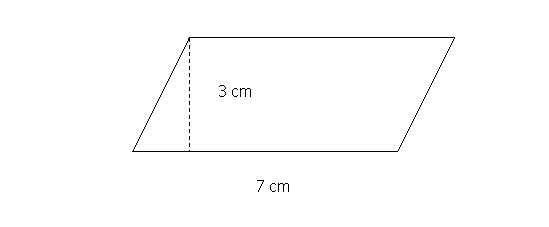
Objetivos de la tarea:
§ Trabajar la combinación de un procedimiento geométrico con uno numérico. El primero será utilizado con objeto de facilitar el cálculo del área. El segundo para determinar la medida del área.
§ Trabajar el procedimiento geométrico de descomposición conveniente de la superficie con posterior reconfiguración por complementariedad de formas.
§ Trabajar el procedimiento numérico: uso de la fórmula para el cálculo del área del rectángulo, que requiere del uso de una unidad de medida unidimensional.
§ Trabajar el área como producto de dos dimensiones lineales.
§ Trabajar el área del paralelogramo como el área del rectángulo de igual base y altura.
Tarea 6PNuu (Tarea 7MApd) (Tarea 10MAma) (Tarea 8A-P)
Paco es jardinero, y ha recibido el encargo de diseñar junto a una casa
un jardín de
a) Dibuja los diferentes jardines que
puede diseñar Paco.
b) Si los dueños de la casa le
informan a Paco que sólo disponen de
Objetivos de la tarea:
§ Trabajar el procedimiento numérico: uso de la fórmula para el cálculo del área del rectángulo, que requiere del uso de una unidad de medida unidimensional.
§ Trabajar el área como producto de dos dimensiones lineales.
§ Trabajar la disociación del área de la forma de la superficie.
§ Trabajar el área del perímetro: superficies de igual área, poseen diferentes perímetros.
¿Te
interesa bajarte/imprimir estas actividades y otras similares para trabajar con
tus alumnos? IR A TAREAS