OBTENCIÓN
DE FÓRMULAS PARA EL CÁLCULO DE ÁREAS
La secuencia
didáctica que se presenta a continuación tiene por objeto:
§
Hacer
ver a los alumnos la necesidad de buscar métodos alternativos, al recuento de
unidades de área, que recubren la superficie, para calcular las áreas de las
figuras planas.
§
Llegar
a la fórmula para el cálculo del área de un rectángulo.
§
Deducir
la fórmula para el cálculo del área del paralelogramo, a partir de la del
rectángulo.
§
Deducir
la fórmula para el cálculo del área del triángulo, a partir de la del
rectángulo.
TAREA 1
Determina el área
de cada una de las figuras siguientes:
![]()
![]() Extraída de Peterson
(1973)
Extraída de Peterson
(1973)
Objetivo de la tarea:
Plantear la necesidad
de la búsqueda de un método alternativo al conteo de unidades de medida que
recubren el rectángulo, al enfrentar a los alumnos al tedio del recuento de las
unidades cuadradas que recubren la figura C.
TAREA 2
Determina el área
de cada una de las figuras siguientes
Extraída de Peterson (1973)
Objetivo de la tarea:
Plantear la necesidad
de la búsqueda de un método alternativo al conteo de unidades cuadradas que
recubren las distintas figuras dadas, al comprobar que ello no proporciona una
medida exacta del área, sino una estimación de ella, además de la dificultad
que entraña el propio recuento.
TAREA 3
Considerando la
longitud del lado del cuadrado como unidad de longitud y el cuadrado como
unidad de área, completa la siguiente tabla:
|
Rectángulo |
Longitud de la base |
Longitud de la altura |
Área |
A
|
|
|
|
|
B |
|
|
|
|
C |
|
|
|
|
D |
|
|
|
|
E |
|
|
|
A B![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()

![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()

Extraída de Peterson (1973)
Objetivo de la tarea:
Relacionar el
número de unidades cuadradas que recubren el rectángulo con la longitud de la
base y la altura de éste.
TAREA 4
Calcula el número
de unidades cuadradas que recubren el rectángulo de la figura y represéntalos.
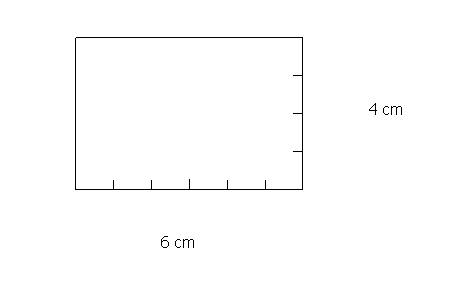
Objetivos de la tarea:
§
Determinar
el número de unidades cuadradas que recubren el rectángulo a partir del
producto de las longitudes de su base y su altura.
§
Observar
que las longitudes de los lados del rectángulo, determinan el número de
unidades cuadradas que “caben” en cada lado y en consecuencia en el interior
del rectángulo.
TAREA 5
a) Compara el
área del rectángulo y del paralelogramo, dados. ¿Poseen la misma área?
Justifica tu respuesta.

b) Calcula el
área del paralelogramo, con los datos que se proporcionan en la figura.
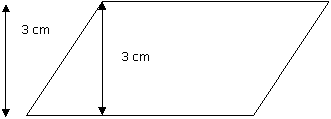

![]()
![]()
Objetivos
de la tarea:
§
Determinar
que el área del paralelogramo es la misma que la del rectángulo de igual base y
altura.
§
Determinar
que el área del paralelogramo se obtiene de multiplicar su base por su altura.
TAREA 6
a) Construye un
rectángulo de igual área que el paralelogramo dado. Indica sus dimensiones.

b) Calcula el
área del paralelogramo.
Objetivos
de la tarea:
§
Concluir
que el área del paralelogramo es la misma que la del rectángulo de igual base y
altura.
§
Concluir
que el área del paralelogramo se obtiene de multiplicar su base por su altura.
TAREA 7
a) Determina en
cada caso el área del triángulo y del rectángulo:

b)
Determina el área de cada triángulo:
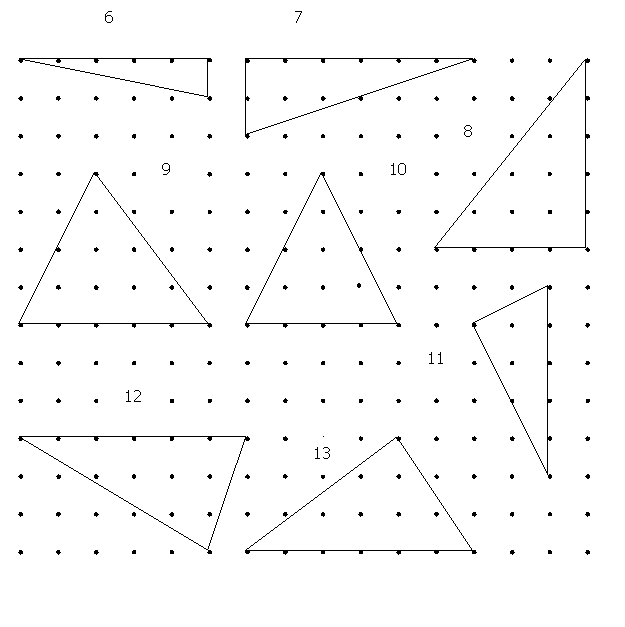
Adaptada de una
actividad de SMP 11-16 (1985)
Objetivo de la tarea:
§
Determinar
que el área del triángulo es la mitad de la del rectángulo de igual base y
altura, que lo contiene.