|
MANIFESTACIONES DEL ÁREA |
|||
|
El área como cantidad de plano ocupado
por la superficie |
El área como magnitud autónoma |
El área como número de unidades que
recubren exactamente la superficie |
El área como producto de dos
dimensiones lineales |
La
manifestación del área como cantidad de plano ocupado
por la superficie es la primera con la que los niños deben estar
familiarizados.
§
Se trabajará realizando tareas de
comparación de áreas de superficies, mediante el uso de procedimientos de naturaleza geométrica, donde el número está
ausente de cualquier razonamiento.
Tareas
Tarea 1MAcp (Tarea 11PG)
La casa de Paco y la de Hugo tienen un corral donde se crían las gallinas. Dibújate los corrales en un folio y recórtalos. ¿En cuál de los dos corrales hay más espacio para que se muevan las gallinas?
Nota.- Se proporcionará a los alumnos una
copia de estas superficies para que puedan manipularlas.
Objetivos de la tarea:
§
Trabajar el área como cantidad de plano ocupado por la
superficie.
§
Trabajar los procedimientos geométricos de: i)
Comparación directa por superposición de las superficies; ii) Comparación
indirecta por recorte y pegado de las piezas en las que queda descompuesta la
superficie.
Tarea 2MAcp (Tarea 7Mama) (Tarea 12PG)
Imagínate que estas figuras representan dos campos
cubiertos de hierba. ¿Tiene el campo A la misma cantidad de hierba que el campo
B?
Nota.- Se proporcionará al alumno rectángulos iguales a los que
constituyen la figura B.
Objetivos de la tarea:
§
Trabajar el área como cantidad de plano ocupado por la
superficie.
§
Trabajar la disociación entre el área y la forma de la
superficie.
§
Trabajar la conservación de área.
§
Romper con la creencia muy extendida en los niños, que
una figura más larga tiene mayor área, al fijarse en una única dimensión.
§
Trabajar los procedimientos geométricos de: i)
Comparación indirecta por recorte y pegado de las piezas en las que queda
descompuesta la superficie. ii) Reconfiguración por complementariedad de formas
de las partes en las que se ha dividido la superficie.
¿Te interesa
bajarte/imprimir estas actividades y otras similares para trabajar con tus
alumnos? IR A TAREAS
|
MANIFESTACIONES DEL ÁREA |
|||
|
El área como cantidad de plano ocupado
por la superficie |
El área como magnitud autónoma |
El área como número de unidades que
recubren exactamente la superficie |
El área como producto de dos
dimensiones lineales |
Por área como magnitud autónoma entendemos el área disociada
de la forma de la superficie y del número que la mide.
La disociación
del área de la forma de la superficie ayuda a disociar el área del
perímetro. La confusión entre el área y el
perímetro es una de las más habituales y más arraigada entre los
estudiantes, que les lleva a cometer frecuentes errores.
- Se trabajará realizando tareas de comparación
de áreas de superficies, de modo que se observe que superficies de forma
diferente pueden tener igual área, mediante el uso, tanto, de procedimientos de naturaleza geométrica como
de naturaleza numérica.
La disociación
del área del número que la mide es clave en la comprensión del papel que
juega la unidad de medida, y en consecuencia en la comprensión del proceso de
medida.
- Se
trabajará realizando tareas de medida del área de una misma superficie,
con el uso de diferentes unidades de medida.
Tareas
Tarea 1Mama (Tarea 5MAcp) (Tarea 13PG)
El tangram es un puzzle de siete piezas que procede de China, y con el que se pueden construir más de 300 figuras diferentes. Las siete piezas resultan de la descomposición del cuadrado como se indica en la figura.
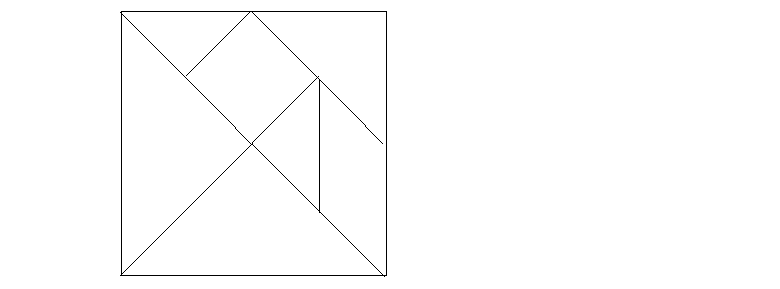
Construye con las siete piezas del tangram cada una de las figuras que a continuación se te presentan. Una vez construidas debes reproducirlas en tu libreta, indicando la posición de las piezas. Responde de forma razonada a la siguiente pregunta: ¿tienen todas estas figuras la misma área?
Nota.- Cada alumno debe disponer de un tangram.
Extraída de Corberán (1996). Dibujos extraídos de
Read (1965)
Objetivos de la tarea:
§
Trabajar la disociación entre el área y la forma de la
superficie.
§
Trabajar el área como cantidad de plano ocupado por la superficie.
§
Trabajar la conservación de área.
§
Romper con la creencia muy extendida en los niños, que
una figura más larga tiene mayor área, al fijarse en una única dimensión.
§
Trabajar el procedimiento geométrico de recorte y pegado
de las piezas en las que queda descompuesta la superficie.
Tarea 2MAma (Tarea 6MAurs) (Tarea 11PNub)
Luís ha diseñado las siguientes figuras,
utilizando para ello cuadrados. Calcula cuántos cuadrados serán necesarios para
construir cada una de estas figuras. ¿Qué observas?
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A |
|
|
|
|
|
|
|
|
|
B |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
C |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
E |
|
|
|
|
|
|
|
|
D |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Adaptada de Horak & Horak (1982)
Objetivos de la tarea:
§
Trabajar la disociación entre el área y la forma de la
superficie.
§
Trabajar el área como número de unidades que recubren la
superficie.
§
Trabajar procedimientos numéricos con uso de una unidad
bidimensional.
Tarea 3Mama (Tarea 7MAurs) (Tarea 12PNub) (Tarea 4UM)
a)
Mide el área de la superficie (S), utilizando las
unidades A, B, C y D. Completa la tabla siguiente:
|
|
Medida del área de
(S) |
|
unidad “A” |
|
|
unidad “B” |
|
|
unidad “C” |
|
|
unidad “C” |
|
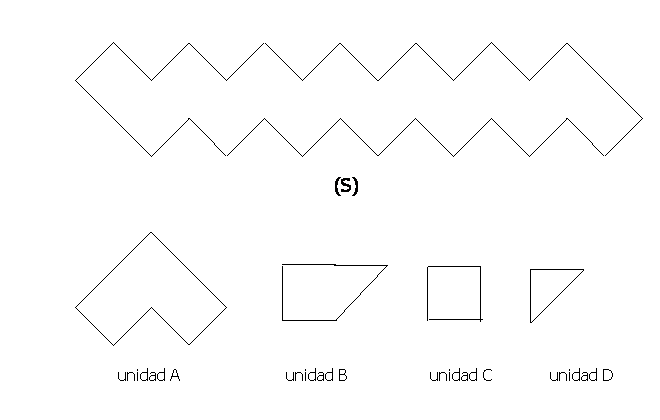
b) Completa la tabla:
|
|
Unidades |
|||
|
A |
B |
C |
D |
|
|
Objeto geométrico |
|
|
|
|
|
A |
|
|
|
|
|
B |
|
|
|
|
|
C |
|
|
|
|
|
D |
|
|
|
|
Nota.- Los alumnos dispondrán de una fotocopia de la superficie (S) y un juego con varias unidades A, B, C y D, del material que se pueda disponer: cartulina, plástico, ...
Extraída de Peterson (1973)
Objetivos de la tarea:
§
Trabajar la disociación del área del número que la mide.
§
Trabajar el área como número de unidades que recubren la
superficie.
§
Trabajar las propiedades de la unidad de medida de área
bidimensional: i) Carácter de recubrimiento de la unidad de medida; ii)
Relación inversa entre el número de unidades que recubren la superficie y el
tamaño de la unidad; iii) Carácter de no discretitud de la unidad.
§
Trabajar procedimientos numéricos con uso de una unidad
bidimensional.
¿Te interesa
bajarte/imprimir estas actividades y otras similares para trabajar con tus
alumnos? IR A TAREAS
|
MANIFESTACIONES DEL ÁREA |
|||
|
El área como cantidad de plano ocupado
por la superficie |
El área como magnitud autónoma |
El área como número de unidades que
recubren exactamente la superficie |
El área como producto de dos
dimensiones lineales |
Para que el
alumno entienda el área como número de unidades que
recubren la superficie, es necesario que éste comprenda el papel que
juega la unidad de medida en el cálculo de áreas.
Estudiar esta manifestación del área, ayudará a los alumnos a enfrentarse significativamente al estudio del área como resultante del producto entre magnitudes lineales.
- Se
trabajará realizando tareas de medición basadas en la comparación de las
áreas de dos superficies, una, la superficie cuya área se desea medir y la
otra, la considerada como unidad, utilizando procedimientos
de carácter numérico con uso
de una unidad de medida bidimensional. De este modo la medida del área
vendrá dada por el número procedente de un recuento o conteo del número de
unidades o fracción de ésta que recubren exactamente la superficie.
Tareas
Tarea 1MAurs (Tarea 13PNub)
Utiliza
tu propia mano y ayudándote de ella, calcula el número de veces que te cabe en
la pizarra de tu clase. El número que has obtenido representa una medida
aproximada del área de la pizarra. Compara la medida que tú has obtenido con la
que han obtenido tus otros compañeros y comentad lo ocurrido.
Objetivos de la tarea:
§
Trabajar el área como número de unidades que recubren la
superficie.
§
Trabajar procedimientos numéricos con uso de una unidad
bidimensional (iteración de una unidad física de medida).
Tarea 2MAurs (Tarea 8Mama) (Tarea 14PNub)
¿Cuántas figuras A necesitarás para cubrir B?
¿Cuántas figuras A necesitarás para cubrir C?
¿Qué puedes decir del área de las figuras B y C?
¿Cuántas figuras A necesitarás para cubrir D?
¿Cuántas figuras B necesitarás para cubrir D?
¿Cuántas figuras C necesitarás para cubrir D?
¿Podrías decir cuál es el área de la figura D?
Nota.- Los alumnos deben tener el conjunto de
formas rectangulares, que se muestran en la figura anterior, por ejemplo hechas
de cartulina, pero no debe aparecer en ellas las medidas.
Adaptada
de Leutzinger & Nelson (1980).
Objetivos de la tarea:
§
Trabajar el área como número de unidades que recubren la
superficie.
§
Trabajar la disociación del área del número que la mide.
§
Trabajar procedimientos numéricos con uso de una unidad
bidimensional: iteración de una unidad física de medida.
Tarea 3MAurs (Tarea 15PNub)
Dibuja tu mano en una hoja de papel cuadriculado y
calcula el número de cuadrados que hay en su interior. Intercambia este dato
con tus compañeros. Después de ello, ¿podrías decir qué niño tiene la mano más
grande y la más pequeña?
Objetivos de la tarea:
§
Trabajar el área como número de unidades que recubren la
superficie.
§
Sugerir la medida del cuerpo para la estimación de áreas.
§
Trabajar técnicas para estimar el área de superficies no
poligonales.
§
Trabajar procedimientos numéricos con uso de una unidad
bidimensional.
¿Te interesa
bajarte/imprimir estas actividades y otras similares para trabajar con tus
alumnos? IR A TAREAS
|
MANIFESTACIONES DEL ÁREA |
|||
|
El área como cantidad de plano ocupado
por la superficie |
El área como magnitud autónoma |
El área como número de unidades que
recubren exactamente la superficie |
El área como producto de dos
dimensiones lineales |
Antes de
abordar el estudio del área como producto de dos
dimensiones lineales, es conveniente tener presente que a pesar de ser
este el enfoque del área más universalmente enseñado a los alumnos,
paradójicamente es el que posee las más altas cotas de incomprensión. Debemos
ser conscientes del nivel de abstracción y de formalización que requiere la medición
de un área mediante cálculos a partir de las dimensiones lineales y de ahí la dificultad de comprensión por parte de los alumnos
de las fórmulas para el cálculo del área de
algunas superficies.
- Se trabajará
realizando tareas de cálculo de áreas de superficies poligonales que
puedan ser descompuestas en rectángulos y/o triángulos, utilizando para
ello la fórmula para el cálculo del área de estos polígonos.
Tareas
Tarea 1MApd (Tarea 10PNuu)
Calcula el área de las figuras A y B.
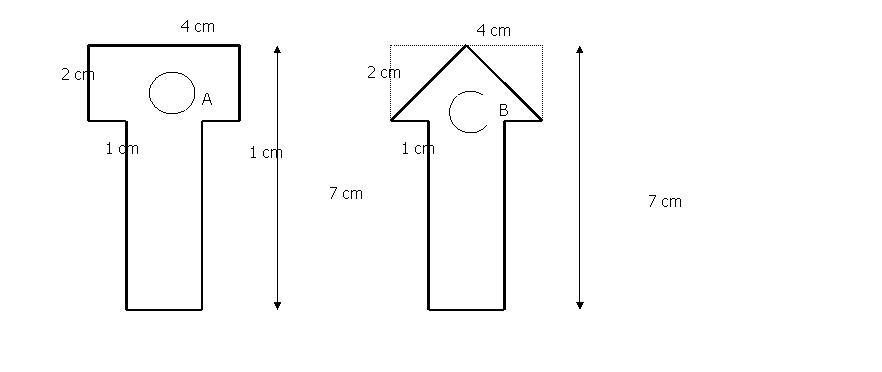
Objetivos de la tarea:
- Trabajar
el área como producto de dos dimensiones lineales.
- Trabajar
procedimientos numéricos con uso de unidad unidimensional.
- Calcular
el área de un triángulo como la mitad del área del rectángulo de igual
base y altura que lo contiene.
- Trabajar
la propiedad aditiva del área.
Tarea 2MApd (Tarea 11PNuu)
Calcula el área de la figura
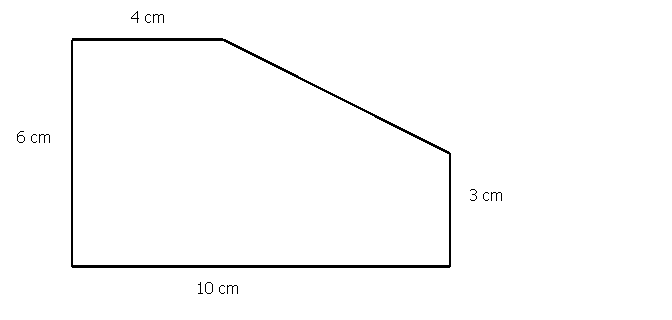
Objetivos de la tarea:
- Trabajar
el área como producto de dos dimensiones lineales.
- Trabajar
procedimientos numéricos con uso de unidad unidimensional.
- Calcular
el área de un triángulo como la mitad del área del rectángulo de igual
base y altura que lo contiene.
- Trabajar
la propiedad aditiva del área.
Tarea 3MApd (Tarea 12PNuu)
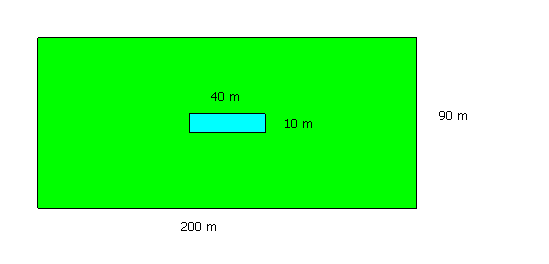
El siguiente dibujo representa el parque donde
juega todos los días Carla. En él, existe en el centro una gran fuente
rectangular. Determina la cantidad de zona ajardinada en la que puede jugar
nuestra amiga.
Objetivos de la tarea:
- Trabajar
el área como producto de dos dimensiones lineales.
- Trabajar
procedimientos numéricos con uso de unidad unidimensional.
- Trabajar
la propiedad aditiva del área.
¿Te interesa
bajarte/imprimir estas actividades y otras similares para trabajar con tus
alumnos? IR A TAREAS