LAS FÓRMULAS PARA EL CÁLCULO DE ÁREAS:
errores y dificultades
El tratamiento
habitual que recibe el área en la enseñanza, se suele limitar en el nivel de
primaria y secundaria al estudio de las fórmulas para el cálculo de áreas, y en
secundaria post-obligatoria (bachilleratos) al estudio de
Se ha constatado
que para una mayoría de alumnos de primaria el área se reduce a la expresión
“longitud x anchura” y a una fórmula para determinar el área del círculo.
Este tipo de
enseñanza conduce a los alumnos ha desarrollar una pobre concepción numérica
del área, asociando ésta a un fórmula de cálculo. Esta extrema pobreza de su
instrucción contrasta con su rico contexto en la naturaleza, la cultura y la
sociedad.
Algunos
investigadores advierten que limitar la enseñanza del área a las fórmulas para
su cálculo, se convierte para los alumnos en un obstáculo para comprender el área como número de unidades que
recubren la superficie y para desarrollar el área como una propiedad que se
conserva por recorte y pegado.
También se ha
observado, que con la enseñanza de las fórmulas se origina un empobrecimiento
en los alumnos, en tanto que éstos abandonan otras técnicas de medida que
utilizan con éxito hasta ese momento, antes de que hayan podido comprender las
fórmulas.
Por otro lado, es
paradójico, que a pesar de ser este enfoque del área el más universalmente
enseñado a los alumnos, se haya constatado en diversas investigaciones, que es
el que posee las más altas cotas de incomprensión por parte de los alumnos.
Son frecuentes
los errores cometidos por los alumnos al utilizar las fórmulas. Se observa
dificultad e incluso incapacidad de utilizarlas para calcular áreas de
superficies poligonales sencillas o para aplicarlas con éxito a la resolución
de problemas relativamente sencillos y que pueden requerir algo más que una
sustitución de un número dentro de una fórmula.
Veamos algunos
ejemplos, que ponen de manifiesto algunos de los errores más habituales que comenten los alumnos:
§
Cuando
le preguntas a los alumnos por una determinada fórmula, por ejemplo, la del
círculo, dan sin mayor problema una expresión que nunca podría corresponder a
una magnitud bidimensional como es el área, como por ejemplo: A = 2πr o A = πr o
A = 2 πr3.
O bien, algunos alumnos cuando se les pide el
área, por ejemplo, de un triángulo del que se conocen las dimensiones de los
tres lados, al no recordar cómo es la fórmula, multiplican las tres
dimensiones.
Este tipo de respuestas pone de manifiesto que los alumnos no reflexionan sobre el
carácter dimensional de las fórmulas.
§ Es frecuente
entre los alumnos la creencia de que si por ejemplo, el área de un cuadrado se
reduce a la mitad, también lo hace la longitud del lado del cuadrado. O bien,
que si los lados de un cuadrado se duplican, también se duplicará el área.
Es decir, extienden la modificación sufrida por la longitud de los lados de la figura al
área de la misma o viceversa. Ello pone de manifiesto, que los alumnos no entienden la relación que existe entre el área, magnitud
bidimensional y las magnitudes unidimensionales a partir de las que se obtiene.
§
Son muy pocos los alumnos que son capaces de utilizar las
fórmulas para comparar el área de dos superficies, centrando su análisis en los
elementos de los que va a depender el área de esa superficie.
Por ejemplo: a los alumnos se les pidió que compararan el área de los dos triángulos de la figura
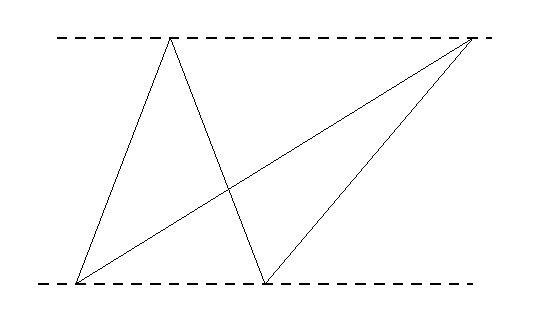
La mayoría de alumnos da una respuesta incorrecta, o manifiesta no poder concluir nada, dado que no dispone de datos numéricos, que le permiten determinar la medida de las áreas, y así poder compararlas. Muy pocos son los alumnos, que responden que los dos triángulos tendrán la misma área, ya que posen la misma base y la misma altura.
Los alumnos limitan el uso de las fórmulas a su
aplicación inmediata, sustituyendo las dimensiones por las medidas dadas, para
realizar un cálculo “rutinario” que el proporcionará la medida buscada, sin comprender que la una fórmula proporciona
la información sobre los elementos de la superficie, de los que va a depender
el área de esta.
Así pues, es necesario tener en cuenta a la hora de abordar la enseñanza de
las fórmulas para el cálculo de áreas, la complejidad de éstas, dado que una
fórmula establece la relación entre magnitudes de distinta naturaleza, una
bidimensional (el área) y otras unidimensionales (longitudes), idea ésta
conceptualmente compleja y difícil de comprender para una mayoría de alumnos,
si no se les prepara para ello.
Por todo lo
expuesto se propone que:
§
La
enseñanza del área no se limite a la enseñanza de las fórmulas para su cálculo.
§
No
introducir el uso de las fórmulas antes de que los alumnos estén familiarizados
con el área como cantidad de plano, como magnitud autónoma y como número de
unidades que recubren la superficie.
§
Estudiar
en contextos geométricos el área de superficies planas, analizando los
elementos de los que depende el área.
§
Estudiar
el carácter bidimensional de las fórmulas del área.