Texto anexo al apartado de Características numéricas.
Relaciones
Relaciones ya estudiadas
Este camino de actividad retoma relaciones entre el tetraedro
y el cubo y el cubo y el dodecaedro (T–C y C¬–D) que ya se han
establecido en Puzzles y estructuras
rígidas. Relaciones
Al examinarlas de nuevo se plantean algunas cuestiones:
¿Qué se ha estudiado respecto del tetraedro y el cubo? ¿Y
del cubo y el dodecaedro?
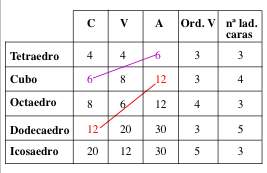
¿Los números de la tabla que remarcan relaciones
entre estos pares de poliedros se podían haber interpretado desde
lo que ya se sabía de estos pares de poliedros?
¿Qué otros números podríamos
explicar con lo que sabemos del tetraedro y el cubo? ¿Y al considerar
el cubo y el dodecaedro? |
|
La respuesta {18}, en la que se remarca cómo se olvida lo que
ya se ha tratado en otro contexto y la necesidad de los modelos para
paliar problemas de visualización es muy representativa de lo
que responden los estudiantes cuando se centra la atención en
las relaciones T–C y C¬–D. Tratar de nuevo la inscripción
del T–C y C-D en este contexto afianza lo visto anteriormente.
|
 
figura 21
|
Además se puede reflexionar sobre la dificultad que conlleva
la descripción de las relaciones de inscripción entre pares de
poliedros regulares al abordarlas en tres contextos diferentes: cuando se construyen
en un contexto de puzzles, cuando surgen por el intento de dar rigidez al cubo,
o cuando se conjeturan a partir de datos numéricos.
Los estudiantes que han participado en nuestra investigación
estaban totalmente de acuerdo en que es necesario haber visto los modelos para
poder imaginarlos y que nunca los hubieran conjeturado de la tabla si los modelos
no los hubieran estudiado antes. Algunos apuntaron además que incluso
después de haberlos trabajado no se habían fijado en que para
esos pares de poliedros, desde la tabla, también se podían destacar
relaciones. Indicaron también dificultades de ellos mismos y trabajo
previo que puede paliarlas.
| {1} |
E1: Los modelos de pares de poliedros inscritos
en los que ambos son armazones yo no podía imaginarlos. Una clase
pasada me sentí mal porque en un modelo como éste, que partía
del cubo [se refiere a un tetraedro inscrito en un cubo siendo los dos
armazones], no conseguía ver absolutamente nada. Después
de haber trabajado las clases anteriores con puzzles y con un modelo en
un armazón [se refiere al de la figura anterior] ya veo bien el
tetraedro en el cubo. No es necesario que apoye el cubo en un vértice
que entonces se ve mejor. |
| {2}: |
E2: Es que tienes que reconocer muy bien los poliedros
regulares apoyados en cara, vértice y arista porque cuando el poliedro
de fuera lo pones como tú lo reconoces mejor, entonces el poliedro
inscrito está apoyado en un elemento que no es como tú lo
has visto antes. Ha venido muy bien que al estudiar los poliedros regulares
los miráramos también apoyados en una arista. Así,
cuando el tetraedro y el dodecaedro están apoyados en una arista
el cubo se reconoce fácil. Cuando el cubo está apoyado en
un vértice, el tetraedro se reconoce bien |
| {3} |
E3: A mi me ha venido bien recordar que en mi grupo construimos los puzzles
con las las pirámides que hay que añadir al tetraedro para
obtener el cubo y los casquetes que hay que añadir al cubo para obtener
el dodecaedro. |
| {4} |
E1: Pues a mi me han venido bien las láminas con dibujos
de estos modelos que nos diste, porque los modelos éstos yo no los
tengo en casa y si no lo repaso, sólo con lo que veo aquí
no tengo suficiente. |
Parte del trabajo previo al que se hace referencia en {1} a {3}
se trata en Buscar las características,
opción que se ofrece al principio de esta investigación, en el
apartado ¨Rompiendo¨ las ideas de cara y...
y en la opción Puzzles y estructuras rígidas.
Relaciones de este apartado. Cabe insistir también en cómo
el estudio de los modelos en diferentes contextos y tiempos diferentes les familiariza
con ellos.