Untitled Document

Texto anexo al apartado de Características numéricas. Relaciones

Buscar las características

Las características numéricas de los poliedros regulares se descubren en un contexto de construcción de modelos y armazones con material comercializado. Remitimos al apartado La construcción y ... en el que se incluyen protocolos que explican las maneras que indicamos para construir algunos poliedros regulares o sugieren cómo descubrirlas en un contexto de construcción.

La construcción de modelos a partir de polígonos centra la atención en la forma de las caras, orden de los vértices (número de caras que se juntan en los vértices), en el número de caras y su disposición en el espacio cuando los modelos se apoyan en diferentes elementos. Las reglas que se dan para la construcción de poliedros regulares son: se construyen con polígonos iguales, con polígonos regulares y en los vértices de cada modelo se juntan el mismo número de polígonos. Comenzamos pues preguntándonos sobre los polígonos regulares que se pueden utilizar y sobre el número de polígonos que se pueden juntar en los vértices. Y cuando se han construido modelos para las posibilidades que hemos delimitado, anotamos otras características de ellos.

Utilizando solo triángulos equiláteros y colocando 3 en cada vértice, se forma una esquina de 3 triángulos que al cerrarla con otro triángulo, obtenemos la pirámide de 4 caras; se obtiene el tetraedro. El tetraedro también se puede construir con dos unidades de dos triángulos que se encajan.

Al juntar 4 triángulos en cada vértice, podemos construir dos picos con 4 triángulos cada uno, y al juntarlos se obtiene el octaedro.

El modelo también puede obtenerse construyendo una cinta con 6 triángulos equiláteros, formamos con ella un anillo y encerramos un espacio con un triángulo equilátero a cada lado.

O construyendo dos casquetes, formados por un triángulo equilátero bordeado con otros 3, y juntando luego estos casquetes.

Juntar 5 triángulos en cada vértice nos lleva al icosaedro. Para ello, se comienza construyendo un pico con 5 triángulos y se continúa de manera que en todos los vértices siempre se junten 5 triángulos hasta que se encierre perfectamente un espacio.

O se construye un pico formado por 5 triángulos, una cinta de 10 triángulos, y otro pico de 5 triángulos.

O se construyen dos casquetes, formados por un pico de 5 triángulos bordeados con otros 5, y juntando luego estos casquetes.

Juntando 6 triángulos en cada vértice queda un hexágono plano. No se puede, por tanto hacer un poliedro así.

Para construir estos poliedros debemos utilizar 4, 8 y 20 triángulos, respectivamente. Esto explica los nombres de los poliedros obtenidos: tetra hace referencia a 4, octa hace referencia a 8, e icosa hace referencia a 20; edro hace referencia a cara.

Utilizando solo cuadrados y colocando 3 en cada vértice obtendremos el hexaedro o cubo. Nos harán falta 6 cuadrados para que se cierre. También se puede construir con 2 picos que se han construido con 3 cuadrados cada uno. Después se juntan estos picos.

Juntando 4 cuadrados en cada vértice, queda un cuadrado más grande. No se puede, por tanto hacer un poliedro así.

Utilizando solo pentágonos regulares y colocando 3 en cada vértice obtendremos el dodecaedro. También se puede construir con dos casquetes iguales, que se obtienen bordeando un pentágono con otros 5. Después se juntan estos casquete. El nombre se explica porque dodeca significa doce, y para construir el modelo se necesitan 12 pentágonos: 6 para cada casquete.Nos harán falta 12 pentágonos regulares para que se cierre. No se pueden juntar 4 pentágonos en un vértice porque el cuarto no cabe en el hueco que dejan los tres primeros.

Utilizando solo hexágonos regulares y colocando 3 en cada vértice obtendremos una figura plana. No se puede, por tanto hacer un poliedro así.

La construcción de armazones de los poliedros regulares incide en las aristas y los vértices y en su disposición en el espacio.

En este contexto de construcción se descubre que para construir el armazón del tetraedro se necesitan 6 varillas y 4 bolitas. Las varillas se juntan de 3 en tres en los vértices. El armazón del octaedro surge utilizando 12 varillas iguales, de manera que en cada bolita siempre se junten 4 varillas. Para ello se necesitan 6 bolitas. Utilizando también 12 varillas iguales pero juntándolas de 3 en 3, surge el armazón del cubo. Para construir el armazón del icosaedro se necesitan 30 varillas iguales que se juntan con bolitas de 5 en 5. Se necesitan 12 bolitas. Y para construir el armazón del icosaedro también se necesitan 30 varillas iguales que al juntarse de 3 en 3 requieren de 20 bolitas.

Como se muestra en el apartado de La construcción y ... el profesor tiene que dirigir la actividad para que se vayan considerando los elementos por niveles, aprovechándolo para enseñar a contar estos elementos de manera estructurada. Conocer diferentes disposiciones espaciales de los elementos de un poliedro porque se apoya en cara, vértice y arista puede llevar a utilizar diferentes estrategias para hallar estos números así como a subrayar determinadas secciones del poliedro que quedan más o menos claras según la posición.

Por ejemplo, para construir el armazón del octaedro se puede comenzar construyendo un triángulo, a cada vértice le añadimos dos varillas, que recogemos después de dos en dos formando 3 vértices, que juntamos con 3 varillas formando otro triángulo. Así, las aristas del octaedro, apoyado en cara, se pueden describir de manera estructurada como sigue: 3 formando triángulo, 6 en zig-zag, 3 formando triángulo: 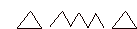Y esta manera de construir el armazón puede llevar también a utilizar la siguiente estrategia para hallar el número de aristas: El octaedro tiene 3 aristas en un nivel (forman triángulo), 6 en otro nivel, pues de cara vértice salen 2 y hay tres vértices, y otras 3 en otro nivel. Pero si el armazón se ha construido a partir de 2 picos de 4 aristas, juntando estos picos con otras 4 que forman un cuadrado, la estrategia utilizada para hallar el número de aristas del octaedro posiblemente se base en esta manera de construir el armazón.

De la misma manera, para el cubo, las aristas del cubo apoyado en vértice se pueden describir como 3 en pico, 6 en zig-zag, 3 en pico: 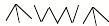. Cuando lo imaginamos apoyado en cara, posiblemente se utilice otra estrategia para contar: 4 formando un cuadrado, otras 4 formando otro cuadrado y las 4 que juntan estos cuadrados.

Construir los armazones del dodecaedro e icosaedro no resulta sencillo si no se han familiarizado previamente con el modelo. Cabe señalar que el armazón del dodecaedro es muy inestable; es muy difícil que las caras del dodecaedro no se deformen. Pero analizando el modelo por niveles, por ejemplo, para los vértices, se pueden distinguir 4 niveles en los que hay 5 vértices que forman pentágonos regulares de dos tamaños. Con lo que su número de vértices es 20.

Para las aristas, se pueden distinguir 5 niveles y así contar como sigue: 5 formando un pentágono (en la cara de arriba), 5 que bajan (que salen de los vértices del pentágono), 10 en la franja central en zig-zag (salen 2 de cada una de las del otro nivel), 5 que bajan y otras 5 que forman otro pentágono opuesto y paralelo al de partida. Así, se puede concluir que para construir el armazón se necesitan 30 varillas iguales y 20 bolitas.

De la misma manera, contando por niveles, imaginando el icosaedro apoyado en vértice, se pueden contar los vértices. Tendrá los dos picos y los de los dos pentágonos que están en diferente nivel. Para contar las aristas se pueden distinguir los niveles siguientes: 5 formando las aristas laterales de la pirámide y otras 5 que forman el pentágono de la base, hay 10 en la franja central en zig-zag (salen 2 de cada uno de los vértices de la base de la pirámide), y luego están las aristas de la base y las aristas laterales de la otra pirámide. Se puede concluir que para construir el armazón se necesitan 30 varillas iguales y 12 bolitas

Cuando el dodecaedro e icosaedro se colocan apoyados en arista se puede centrar la atención en que ambos poliedros tienen 3 pares de aristas opuestas que quedan arriba, abajo, derecha, izquierda, delante y detrás, que cuando se juntan se forman 3 rectángulos que son perpendiculares entre sí.

De esta construcción con polígonos y varillas se pueden hacer también otras observaciones interesantes:

El cubo y el octaedro tienen el mismo número de aristas, 12. El cubo tiene 6 caras y 8 vértices y el octaedro tiene 8 caras y 6 vértices. Las caras del cubo tienen 4 lados y las del tetraedro tienen 3; en los vértices del cubo se juntan 3 caras y 3 aristas y en los vértices del octaedro se juntan 4 caras y 4 aristas.
Asimismo, el dodecaedro y el icosaedro tienen el mismo número de aristas, 30. El dodecaedro tiene 12 caras y 20 vértices y el icosaedro tiene 20 caras y 12 vértices. Las caras del dodecaedro tienen 5 lados y las del icosaedro tienen 3; en los vértices del dodecaedro se juntan 3 caras y 3 aristas y en los vértices del icosaedro se juntan 5 caras y 5 aristas.